题目内容
如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
(1)求证:CF与⊙O相切;
(2)若AD=2,F为AE的中点,求AB的长.

(1)证明:如图所示:连接OF、OC,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,
 ∴AO=
∴AO= AD,EC=
AD,EC= BC,
BC,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形,
∴AE∥OC,
∴∠DOC=∠OAF,∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠DOC=∠FOC,
∵在△ODC和△OFC中
 ,
,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与⊙O相切;
(2)解:如图所示:连接DE,
∵AO=DO,AF=EF,AD=2,
∴DE=20F=2,
∵E是BC的中点,
∴EC=1,
在Rt△DCE中,由勾股定理得:
DC= =
= =
= ,
,
∴AB=CD= .
.


练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目

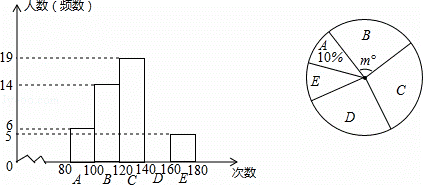
 =90次),则这次调查的样本平均数是多少?
=90次),则这次调查的样本平均数是多少? 3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人? )÷
)÷ ,从﹣1,2,3中选择一个适当的数作为x值代入.
,从﹣1,2,3中选择一个适当的数作为x值代入. x(x﹣1)=21 C.
x(x﹣1)=21 C.  B.
B.  C. ﹣2 D. 2
C. ﹣2 D. 2