Question

【题目】已知的半径是，直线与相交于、两点．是上的一个动点，若，则面积的最大值是________．

Answer 1

【答案】

【解析】

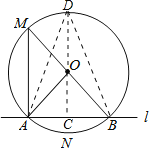
过点O作OC⊥AB于C，交⊙O于D点，连结OA、OB、DA、DB根据圆周角定理推出△OAB为等腰直角三角形，求得AB=OA=2，当M点到AB的距离最大，△MAB的面积最大，即M点运动到D点，问题得解．

过点O作OC⊥AB于C，交⊙O于D点，连结OA、OB、DA、DB如图，

∵∠AMB=45°，

∴∠AOB=2∠AMB=90°，

∴△OAB为等腰直角三角形，

∴AB=OA=2，

∴当M点到AB的距离最大，△MAB的面积最大；即M点运动到D点，

∴△AMB面积的最大值=×ABDC=×2×（2+）=2+2，

故答案为：2+2．