题目内容
如图,抛物线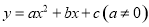 的对称轴是直线
的对称轴是直线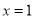 ,有下列结论: (1)
,有下列结论: (1)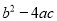 >0;(2)
>0;(2)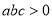 ;(3)
;(3)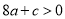 ;(4)
;(4)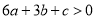 .其中正确结论的个数有( )
.其中正确结论的个数有( )
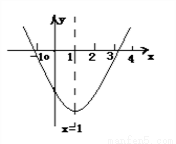
A. 4 B. 3 C. 2 D. 1
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
题目内容
如图,抛物线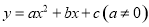 的对称轴是直线
的对称轴是直线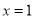 ,有下列结论: (1)
,有下列结论: (1)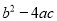 >0;(2)
>0;(2)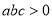 ;(3)
;(3)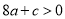 ;(4)
;(4)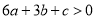 .其中正确结论的个数有( )
.其中正确结论的个数有( )

A. 4 B. 3 C. 2 D. 1
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案