题目内容
17．
如图，BC是⊙O的直径，A是CB延长线上一点，AD切⊙O于点D，如果AB=2，∠A=30°，那么⊙O半径等于（ ）| A． | 2 | B． | $\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | 2$\sqrt{2}$ |
分析 连接OD，则△AOD是直角三角形，根据直角三角形即可求得OD的长．
解答 解：连接OD，
∵AB=2，∠A=30°，
∴设OD=x，则OA=x+2，
∵AD切⊙O于点D，
∴OA=2OD，
∴x+2=2x，
解得：x=2，
故选A
点评 本题主要考查了切线的性质，正确确定题目中未知数的设法是解题的关键．
练习册系列答案
相关题目
9．已知点（x1，-4），（x2，2）都在直线y=$\frac{1}{2}$x+2上，则x1，x2大小关系是（ ）
| A． | x1＞x2 | B． | x1=x2 | C． | x1＜x2 | D． | 不能比较 |
8．
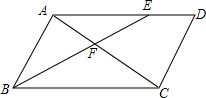如图，在?ABCD中，点E在AD边上，BE交对角线AC于点F，则下列各式错误的是（ ）
如图，在?ABCD中，点E在AD边上，BE交对角线AC于点F，则下列各式错误的是（ ）| A． | $\frac{AF}{CF}=\frac{EF}{BF}$ | B． | $\frac{AF}{BF}=\frac{EF}{CF}$ | C． | $\frac{BF}{BE}=\frac{CF}{AC}$ | D． | $\frac{AF}{EF}=\frac{CF}{BF}$ |
5．下列运算正确的是（ ）
| A． | （ab）2=ab2 | B． | 3a+2a2=5a2 | C． | $\sqrt{（-4）^{2}}$=-4 | D． | a•a=a2 |
12．如图所示，在平面直角坐标系中A（0，0），B（2，0），△AP1B是等腰直角三角形，且∠P1=90°，把△AP1B绕点B顺时针旋转180°，得到△BP2C；把△BP2C绕点C顺时针旋转180°，得到△CP3D．依此类推，则旋转第2015次后，得到的等腰直角三角形的直角顶点P2016的坐标为（ ）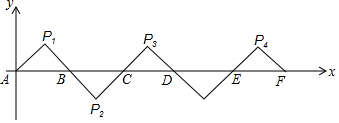
| A． | （4033，-1） | B． | （4031，-1） | C． | （4033，1） | D． | （4031，1） |
2．
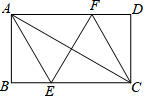如图，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF，若AB=2$\sqrt{3}$，∠DCF=30°，则EF的长为（ ）
如图，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF，若AB=2$\sqrt{3}$，∠DCF=30°，则EF的长为（ ）| A． | 4 | B． | 6 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
9．下列语句中正确的是（ ）
| A． | 数轴上的点都表示有理数 | B． | 若|a|=a，则a是一个非负数 | ||
| C． | -a一定是一个负数 | D． | 离原点越远的数就越小 |
6．室内温度18℃，室外温度-7℃，室外温度比室内温度低（ ）
| A． | 25℃ | B． | 15℃ | C． | -25℃ | D． | -15℃ |
4．
如图，在正方形ABCD中，O为对角线交点，将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF，则在旋转过程中图中阴影部分的面积（ ）
如图，在正方形ABCD中，O为对角线交点，将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF，则在旋转过程中图中阴影部分的面积（ ）| A． | 不变 | B． | 由大变小 | ||
| C． | 由小变大 | D． | 先由小变大，后由大变小 |