题目内容
在△ABC中,AD是BC边上的高,∠B=30°,∠C=45°,CD=2.求BC的长.

2 +2.
+2.
【解析】
试题分析:先在Rt△ACD中,运用正切函数的定义得出AD=CD=2,然后在Rt△ABD中,运用正切函数的定义得出BD=2 ,则根据BC=BD+CD即可求解.
,则根据BC=BD+CD即可求解.
试题解析:∵AD是△ABC中BC边上的高,
∴AD⊥BC,
∴∠ADB=∠ADC=90.
在Rt△ACD中,
∵tanC= =tan45°=1,
=tan45°=1,
∴AD=2.
在Rt△ABD中,
∵tanB= =tan30°=
=tan30°= ,
,
∴BD=2 .
.
∴BC=BD+CD=2 +2,
+2,
即BC的长为2 +2.
+2.
考点:解直角三角形.

练习册系列答案
相关题目



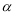 ,直接写出∠ADB的大小(用含
,直接写出∠ADB的大小(用含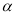 的式子表示);
的式子表示);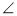 BAC=60°,求证:BD+CD=AD;
BAC=60°,求证:BD+CD=AD;