题目内容
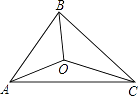
【题目】如图,正方形ABCD的边长为12,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B'处.
(1)当![]() =1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
=1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
(2)当点B'恰好落在对角线AC上时,如图2,此时CF的长为 ; ![]() = .
= .
(3)当![]() =3时,求∠DA B'的正弦值.
=3时,求∠DA B'的正弦值.
【答案】(1)①CF的长为12;②证明见解析;
2)CF的长为12![]() ,
, ![]() =
=![]() ;
;
(3)当![]() 时,∠DA B'的正弦值为
时,∠DA B'的正弦值为![]() 或
或![]() .
.
【解析】解:(1)①CF的长为 12 ;
②证明:∵四边形ABCD为正方形,
∴AB∥CD,∴∠ F=∠ BAF,
由折叠可知:∠ BAF=∠ MAF,
∴∠ F=∠ MAF,∴AM=FM.
(2)CF的长为12![]() ;
;
![]() =
=![]() .
.
(3)①当点E在线段BC上时,如图3,
 A B'的延长线交CD于点M,易证:△ABE∽△FCE,
A B'的延长线交CD于点M,易证:△ABE∽△FCE,
∴![]() ,即
,即![]() ,∴CF=4,
,∴CF=4,
由(1)②证明可知:
AM=FM.设DM=x,则MC=12-x,则AM=FM=16-x,
在Rt△ADM中, ![]() ,
,
 即(16-x)2=122+x2,解得:x=
即(16-x)2=122+x2,解得:x=![]() ,
,
则16-x=16-![]() =
=![]() ,
,
∴sin∠DA B'=![]() =
=![]() .
.
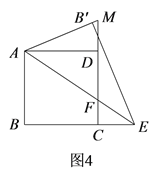
②当点E在BC的延长线上时,如图4,
易证:△ABE∽△FCE,
∴![]() ,即
,即![]() ,∴CF=4,
,∴CF=4,
则DF=12-4=8,设DM=x,则AM=FM=8+x,
在Rt△ADM中, ![]() ,
,
即(8+x)2=122+x2,解得:x=5,则AM=8+x=13,
∴sin∠DA B'=![]() =
=![]() .
.
综上所述:当![]() 时,∠DA B'的正弦值为
时,∠DA B'的正弦值为![]() 或
或![]() .
.

练习册系列答案
相关题目