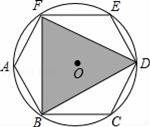
题目内容
如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数
 的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为 .
的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为 .


3 .
【考点】反比例函数系数k的几何意义.
【专题】探究型.
【分析】先设P(0,b),由直线AB∥x轴,则A,B两点的纵坐标都为b,而A,B分别在反比例函数y=﹣
 和y=
和y=
 的图象上,可得到A点坐标为(﹣
的图象上,可得到A点坐标为(﹣
 ,b),B点坐标为(
,b),B点坐标为(
 ,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
【解答】解:设P(0,b),
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,而点A在反比例函数y=﹣
 的图象上,
的图象上,
∴当y=b,x=﹣
 ,
,
即A点坐标为(﹣
 ,b),
,b),
又∵点B在反比例函数y=
 的图象上,
的图象上,
∴当y=b,x=
 ,
,
即B点坐标为(
 ,b),
,b),
∴AB=
 ﹣(﹣
﹣(﹣
 )=
)=
 ,
,
∴S△ABC=
 •AB•OP=
•AB•OP=
 •
•
 •b=3.
•b=3.
故答案为:3.
【点评】本题考查的是反比例函数系数k的几何意义,即在反比例函数y=
 的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
 ,且保持不变.
,且保持不变.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 +3=11-6
+3=11-6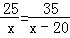 B.
B. C.
C.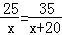 D.
D.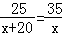



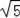
 B.2
B.2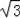

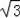

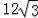
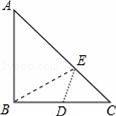
 ,则⊙O的半径为 .
,则⊙O的半径为 .