题目内容
 已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB、AC的距离分别为DE、DF.
已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB、AC的距离分别为DE、DF.(1)当D点在什么位置时,DE=DF?并加以证明.
(2)探索DE、DF与等腰△ABC的高的关系.说明理由.
分析:(1)连接AD,根据三线合一定理求出AD平分∠BAC,根据角平分线性质求出即可.
(2)连接AD,过C作CM⊥AB于M,根据三角形面积公式求出即可.
(2)连接AD,过C作CM⊥AB于M,根据三角形面积公式求出即可.
解答:解:(1)D为中点时,DE=DF,
理由是:
连接AD,
∵AB=AC,D为BC中点,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF.
(2)DE+DF的长为腰上的高的长,
理由是:连接AD,过C作CM⊥AB于M,
∵S△ABC=S△ABD+S△ACD,
∴
AB×CM=
AB×DE+
AC×DF,
∵AB=AC,
∴DE+DF=CM,
即DE+DF的长为腰上的高的长.
理由是:

连接AD,
∵AB=AC,D为BC中点,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF.
(2)DE+DF的长为腰上的高的长,

理由是:连接AD,过C作CM⊥AB于M,
∵S△ABC=S△ABD+S△ACD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴DE+DF=CM,
即DE+DF的长为腰上的高的长.
点评:本题考查了角平分线性质,等腰三角形性质,三角形面积的应用,题目具有一定的代表性,难度适中.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 已知:如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC相交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
已知:如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC相交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F. 23、已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB、AC的距离分别为DE、DF,当D点在什么位置时,DE=DF?并加以证明.
23、已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB、AC的距离分别为DE、DF,当D点在什么位置时,DE=DF?并加以证明.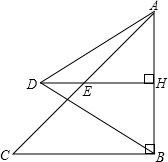 已知,如图:△ABC是等腰直角三角形,∠ABC=90°,AB=10,D为△ABC外一点,连接AD、BD,过D作DH⊥AB,垂足为H,交AC于E.
已知,如图:△ABC是等腰直角三角形,∠ABC=90°,AB=10,D为△ABC外一点,连接AD、BD,过D作DH⊥AB,垂足为H,交AC于E. 23、已知:如图,△ABC是等腰三角形,AB=AC,且∠1=∠2,
23、已知:如图,△ABC是等腰三角形,AB=AC,且∠1=∠2,