题目内容
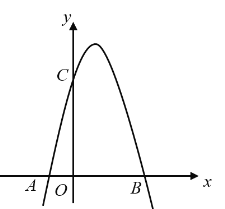
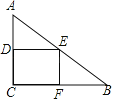
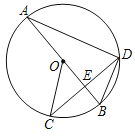
【题目】如图,在![]() 中,
中,![]() 是直径,
是直径,![]() 是弦,
是弦,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接OD,利用圆周角定理得到∠ADB=90°,利用垂径定理得到CE=DE,![]() ,则根据圆周角定理得到∠COE=2∠BAD=∠BOD=50°,所以∠OCE=40°,OE<CE,然后利用∠BOD=50°,∠OBD=65°判断OD>BD,即OC>BD,从而可对各选项进行判断.
,则根据圆周角定理得到∠COE=2∠BAD=∠BOD=50°,所以∠OCE=40°,OE<CE,然后利用∠BOD=50°,∠OBD=65°判断OD>BD,即OC>BD,从而可对各选项进行判断.
解:连接OD,如图,

∵AB为直径,
∴∠ADB=90°,
∵AB⊥CD,
∴CE=DE,![]() ,
,
∴∠COE=2∠BAD=∠BOD=2×25°=50°,
所以C选项正确;
∴∠OCE=40°,所以A选项错误;
∴OE<CE,所以B选项错误;
∵∠BOD=50°,∠OBD=65°,
∴OD>BD,即OC>BD,所以D选项错误.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目