题目内容
5．
如图，已知AB是⊙O的直径，弦CD⊥AB于E，CD=16cm，AB=20cm，求BE的长．
分析 如图，连接OD；由垂径定理求出DE的长度，运用勾股定理列出关于OE的等式，求出OE即可解决问题．
解答 
解：如图，连接OD；
∵弦CD⊥AB，且直径AB=20，CD=16，
∴OD=10，DE=CE=8，
由勾股定理得：OE2=OD2-DE2，
∴OE=6，BE=10-6=4（cm）．
点评 该题主要考查了垂径定理、勾股定理等几何知识点及其应用问题；解题的关键是作辅助线，构造直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
16．
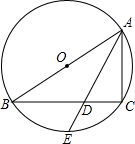如图，AB是⊙O的直径，点C在⊙O上，∠BAC的平分线交⊙O于E，交BC于D．若⊙O的半径为5，AC=6，那么DE的长为（ ）
如图，AB是⊙O的直径，点C在⊙O上，∠BAC的平分线交⊙O于E，交BC于D．若⊙O的半径为5，AC=6，那么DE的长为（ ）| A． | $\frac{9}{5}$$\sqrt{5}$ | B． | $\sqrt{5}$ | C． | 2 | D． | $\sqrt{3}$ |
13．下列式子，一定成立的是（ ）
| A． | 32=6 | B． | -32=9 | C． | |-23|=8 | D． | （-1）8=-1 |
已知：如图，∠B+∠A=180°，则AD∥BC，理由是同旁内角互补，两直线平行；
如图，AB∥DE，若∠B=130°，∠D=30°，则∠BCF=100°．