题目内容
若关于x的方程x2+2mx+m2+3m-2=0有两个实数根x1、x2,则x1(x2+x1)+x22的最小值为 .
考点:根与系数的关系,二次函数的最值
专题:压轴题,判别式法
分析:由题意可得△=b2-4ac≥0,然后根据不等式的最小值计算即可得到结论.
解答:解:由题意知,方程x2+2mx+m2+3m-2=0有两个实数根,
则△=b2-4ac=4m2-4(m2+3m-2)=8-12m≥0,
∴m≤
,
∵x1(x2+x1)+x22
=(x2+x1)2-x1x2
=(-2m)2-(m2+3m-2)
=3m2-3m+2
=3(m2-m+
-
)+2
=3(m-
)2 +
;
∴当m=
时,有最小值
;
∵
<
,
∴m=
成立;
∴最小值为
;
故答案为:
.
则△=b2-4ac=4m2-4(m2+3m-2)=8-12m≥0,
∴m≤
| 2 |
| 3 |
∵x1(x2+x1)+x22
=(x2+x1)2-x1x2
=(-2m)2-(m2+3m-2)
=3m2-3m+2
=3(m2-m+
| 1 |
| 4 |
| 1 |
| 4 |
=3(m-
| 1 |
| 2 |
| 5 |
| 4 |
∴当m=
| 1 |
| 2 |
| 5 |
| 4 |
∵
| 1 |
| 2 |
| 2 |
| 3 |
∴m=
| 1 |
| 2 |
∴最小值为
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查了一元二次方程根与系数关系,考查了一元二次不等式的最值问题.
总结一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
总结一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
以下问题,不适合用全面调查的是( )
| A、旅客上飞机前的安检 |
| B、学校招聘教师,对应聘人员的面试 |
| C、了解全校学生的课外读书时间 |
| D、了解一批灯泡的使用寿命 |
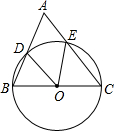 如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE=
如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=
如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=