Question

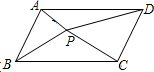如图所示，P为平行四边形内任一点，△PAB，△PBC，△PCD面积分别为3，4，5，则△PAD的面积为（　　）

• A、3
• B、4
• C、5
• D、6

Answer 1

分析：过P作EF⊥AD交AD于E，交BC于F，MN⊥AB交AB于M，交CD于N，根据平行四边形的性质推出AD=BC，AB=CD，AD∥BC，AB∥CD，根据三角形的面积公式S_△PAB+S_△PCD=

1

2

S_{平行四边形}=8即可．

解答：解：过P作EF⊥AD交AD于E，交BC于F，MN⊥AB交AB于M，交CD于N，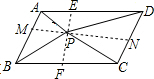
∵四边形ABCD是平行四边形，
∴AD=BC，AB=CD，AD∥BC，AB∥CD，
∴EF⊥BC，MN⊥CD，
∴S_{平行四边形ABCD}=AB×MN=AD×EF，
∵S_△PAB+S_△PCD=

1

2

AB×PM+

1

2

CD×PN=

1

2

AB×MN=

1

2

S_{平行四边形}=3+5=8，
同理：S_△PAD+S_△PBC=

1

2

S_{平行四边形ABCD}=4+S_△PAD，
∴S_△PAD=8-4=4．
故选B．

点评：本题主要考查对平行四边形的性质，三角形的面积等知识点的理解和掌握，能根据性质求出S_△PAB+S_△PCD=

1

2

S_{平行四边形}是解此题的关键．