Question

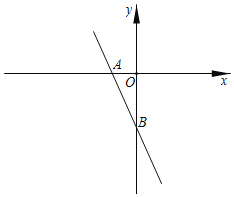
【题目】如图，在平面直角坐标系中，一次函数y＝﹣2x﹣2交x轴于点A，交y轴于点B，若直线BC交x轴于点C，且∠ABC＝45°，则点C的横坐标为_____．

Answer 1

【答案】或﹣6．

【解析】

先算出A点坐标、B点坐标, 作∠ABC1=45°交x轴于点C1,过A作AD⊥BC1,利用面积公式求出C1点,再算出BC1的函数表达式,再求出过点B且垂直于BC的函数表达式,交于x轴的点即为C2点.

如图所示,作∠ABC1=45°交x轴于点C1,过A作AD⊥BC1.

将x=0,代入函数图象解得y=－2,∴B(0,－2).

将y=0,代入函数图象解得x=－1,∴A(－1,0).

根据勾股定理得:AB=.

∵∠ABC1=45°, AD⊥BC1,

∴AD=.

设OC1=a,根据面积公式可得:,

即: ,

平方后可得: ,

整理得: .

利用十字相乘法可得: .

解得或－6(由图舍去)

由B(0,－2),C1(,0),可得BC1函数表达式为:y=3x－2.

作BC2⊥BC1,根据一次函数垂直的性质可得BC2的k值为,且过B(0,－2),

∴BC2的表达式为:y=x－2.

当y=0时,x=－6.

综上所述C点的横坐标为: 或﹣6.