题目内容
 (2013•槐荫区二模)如图,直线y=-
(2013•槐荫区二模)如图,直线y=-
| ||
| 3 |
分析:求得直角△ABO的两条直角边的长,即可利用解直角三角形的方法求得AB,以及∠OAB的度数,则∠OAB′是直角,据此即可求解.
解答:解:在y=-
x+2中令x=0,解得:y=2;
令y=0,解得:x=2
.
则OA=2
,OB=2.
∴在直角△ABO中,AB=
=4,∠BAO=30°,
又∵∠BAB′=60°,
∴∠OAB′=90°,
∴B′的坐标是(2
,4).
故选B.
| ||
| 3 |
令y=0,解得:x=2
| 3 |
则OA=2
| 3 |
∴在直角△ABO中,AB=
| OA2+OB2 |
又∵∠BAB′=60°,
∴∠OAB′=90°,
∴B′的坐标是(2
| 3 |
故选B.
点评:本题考查了一次函数与解直角三角形,正确证明∠OAB′=90°是关键.

练习册系列答案
相关题目
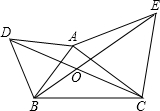 (2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
(2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是 (2013•槐荫区二模)如图,在△ABC中AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分的面积是
(2013•槐荫区二模)如图,在△ABC中AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分的面积是