题目内容
(10分)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.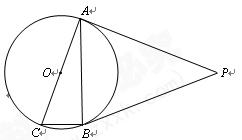
【小题1】(1)试说明:PB是⊙O的切线;
【小题2】(2)已知⊙O的半径为 ,AB=2
,AB=2 ,求PA的长.
,求PA的长.
【小题1】解:(1)连接OB,OP,交AB于点D
∵⊙O是Rt△ABC的外接圆,
∴AC是⊙O的直径.……1分
又∵PA与⊙O相切,∴∠OAP=90°……2分
∵OA=OB,PA=PB,OP=OP
∴△OAP≌△OBP……4分
∴∠OBP=∠OAP=90°,即OB⊥BP.
又∵点B在⊙O上,∴PB是⊙O的切线.……5分
【小题2】(2)∵∠ABC=∠OBP=90°,∴∠OBC=∠ABP
又∵OC=OB,PA=PB, ∴∠OCB=∠OBC=∠ABP=∠BAP∴△OCP∽△PAB……6分
∴ 即
即 ……7分
……7分
而在Rt△ABC中, AB=2 ,AC=2
,AC=2 ∴BC=2……8分
∴BC=2……8分
∴PA= ……9分
……9分
解析

练习册系列答案
相关题目
 7、如图,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有( )
7、如图,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有( ) 如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F.
如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F. 24、如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长.
24、如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长. (2013•顺义区二模)已知:如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(2013•顺义区二模)已知:如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB. 如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5
如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5