题目内容
 如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5
如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5| 3 |
分析:延长AB、DC相交于点E,根据直角三角形两锐角互余求出∠E=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出BE、DE的长,根据勾股定理列式求出CE的长,从而求出DC,再利用勾股定理列式计算即可求出DB.
解答: 解:如图,延长AB、DC相交于点E,
解:如图,延长AB、DC相交于点E,
∵∠ADC=60°,BC=2cm,AD=5
cm,
∴BE=2BC=2×2=4(cm),
DE=2AD=2×5
=10
(cm),
在Rt△BCE中,CE=
=
=2
(cm),
∴DC=DE-CE=10
-2
=8
(cm),
在Rt△BCD中,DB=
=
=14(cm).
 解:如图,延长AB、DC相交于点E,
解:如图,延长AB、DC相交于点E,∵∠ADC=60°,BC=2cm,AD=5
| 3 |
∴BE=2BC=2×2=4(cm),
DE=2AD=2×5
| 3 |
| 3 |
在Rt△BCE中,CE=
| BE2-BC2 |
| 42-22 |
| 3 |
∴DC=DE-CE=10
| 3 |
| 3 |
| 3 |
在Rt△BCD中,DB=
| DC2+BC2 |
(8
|
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理的应用,作辅助线构造出直角三角形是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
 如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F.
如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F.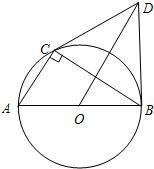 5、如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.
5、如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD. 如图,CD是Rt△ABC斜边AB上的高,且∠B=α,AD=2,BD=x,则用α,x表示图中三角形面积的关系式为
如图,CD是Rt△ABC斜边AB上的高,且∠B=α,AD=2,BD=x,则用α,x表示图中三角形面积的关系式为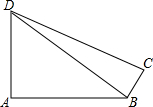 如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5
如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5 cm,求DB、DC的长. (直角三角形中,30°角所对边等于斜边的一半)
cm,求DB、DC的长. (直角三角形中,30°角所对边等于斜边的一半)