题目内容
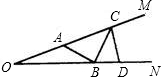 如图,设∠MON=20°,A为OM上一点,OA=4
如图,设∠MON=20°,A为OM上一点,OA=4| 3 |
| 3 |
| A、10 | B、11 | C、12 | D、13 |
分析:先分别作A、D关于ON、OM的对称点A′、D′点,连接A′B、CD′、A′D′,根据对称的性质可得A′B=AB,CD′=CD,再由勾股定理即可求出A′D′的长,由两点之间线段最短可得A′D′的长即为折线ABCD的长的最小值.
解答: 解:如图,分别作A、D关于ON、OM的对称点A′、D′点,连接A′B、CD′、A′D′,OD′,OA′,
解:如图,分别作A、D关于ON、OM的对称点A′、D′点,连接A′B、CD′、A′D′,OD′,OA′,
则A′B=AB,CD′=CD,
∴AB+AC+CD≥A′B+BC+CD′,
显然A′B+BC+CD′≥A′D′,
∵∠A′ON=∠NOM=MOD′=20°,∴∠D′OA′=60°,
又OA′=OA=4
,OD′=OD=8
,即
=
,
而cos60°=
,∴cos60°=
,
∴△D′OA′为直角三角形,且∠OA′D′=90°,
∴A′D′=
,
=
,
=12.
故折线ABCD的长的最小值为12.
故选C.
 解:如图,分别作A、D关于ON、OM的对称点A′、D′点,连接A′B、CD′、A′D′,OD′,OA′,
解:如图,分别作A、D关于ON、OM的对称点A′、D′点,连接A′B、CD′、A′D′,OD′,OA′,则A′B=AB,CD′=CD,
∴AB+AC+CD≥A′B+BC+CD′,
显然A′B+BC+CD′≥A′D′,
∵∠A′ON=∠NOM=MOD′=20°,∴∠D′OA′=60°,
又OA′=OA=4
| 3 |
| 3 |
| OA′ |
| OD′ |
| 1 |
| 2 |
而cos60°=
| 1 |
| 2 |
| OA′ |
| OD′ |
∴△D′OA′为直角三角形,且∠OA′D′=90°,
∴A′D′=
| (OD′)2-(OA′)2 |
=
(8-
|
=12.
故折线ABCD的长的最小值为12.
故选C.
点评:本题考查的是最短线路问题,根据轴对称的性质作出图形是解答此类题目的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
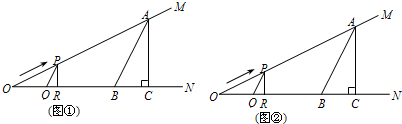
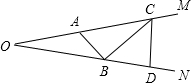 如图,设∠MON=20°,A为OM上一点,OA=4
如图,设∠MON=20°,A为OM上一点,OA=4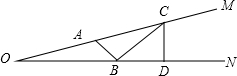
 如图,设∠MON=20°,A为OM上一点,OA=4
如图,设∠MON=20°,A为OM上一点,OA=4 ,D为ON上一点,OD=8
,D为ON上一点,OD=8