题目内容
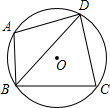 如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,AB=1,BC=2,则AD=
如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,AB=1,BC=2,则AD=考点:圆内接四边形的性质
专题:
分析:连结AC.先由勾股定理求出AC2=AB2+BC2=12+22=5,根据圆周角定理及角平分线的定义得出AD=CD,由圆内接四边形的性质得到∠ADC=180°-∠ABC=90°,那么△ACD是等腰直角三角形,则AD=
AC=
×
=
.作AE⊥BD于E,CF⊥BD于F,则AE=
AB=
,CF=
BC=
.由S四边形ABCD=S△ABD+S△CBD=S△ABC+S△ADC,即可求出BD=
.
| ||
| 2 |
| ||
| 2 |
| 5 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
3
| ||
| 2 |
解答: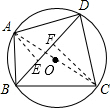 解:如图,连结AC.
解:如图,连结AC.
∵∠ABC=90°,AB=1,BC=2,
∴AC2=AB2+BC2=12+22=5.
∵∠ABC=90°,BD平分∠ABC,
∴∠ABD=∠CBD=45°,
∴
=
,
∴AD=CD,
∵⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,
∴∠ADC=180°-∠ABC=90°,
∴△ACD是等腰直角三角形,
∴AD=
AC=
×
=
.
作AE⊥BD于E,CF⊥BD于F,则AE=
AB=
,CF=
BC=
.
∵S四边形ABCD=S△ABD+S△CBD=S△ABC+S△ADC,
∴
BD•AE+
BD•CF=
AB•BC+
AD•CD,
∴
BD(
+
)=
×1×2+
×
×
,
∴BD=
.
故答案为
,
.
 解:如图,连结AC.
解:如图,连结AC.∵∠ABC=90°,AB=1,BC=2,
∴AC2=AB2+BC2=12+22=5.
∵∠ABC=90°,BD平分∠ABC,
∴∠ABD=∠CBD=45°,
∴
 |
| AD |
 |
| CD |
∴AD=CD,
∵⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,
∴∠ADC=180°-∠ABC=90°,
∴△ACD是等腰直角三角形,
∴AD=
| ||
| 2 |
| ||
| 2 |
| 5 |
| ||
| 2 |
作AE⊥BD于E,CF⊥BD于F,则AE=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
∵S四边形ABCD=S△ABD+S△CBD=S△ABC+S△ADC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴BD=
3
| ||
| 2 |
故答案为
| ||
| 2 |
3
| ||
| 2 |
点评:本题考查了圆内接四边形的性质,圆周角定理,角平分线的定义,直径所对的圆周角是直角,在同圆或等圆中,同弧所对的圆周角相等,勾股定理的应用,四边形的面积,有一定难度.准确作出辅助线是解题的关键.

练习册系列答案
相关题目
某外贸公司要出口一批食品罐头,标准质量为每听450克,现抽取10听样品进行检测,它们的质量与标准质量的差值(单位:克)如下:-10,+5,0,+5,0,0,-5,0,+5,+10,则这10听罐头质量的众数为( )
| A、460 | B、455 |
| C、450 | D、0 |
不能判定两个直角三角形全等的条件是( )
| A、两个锐角对应相等 |
| B、两条直角边对应相等 |
| C、斜边和一锐角对应相等 |
| D、斜边和一条直角边对应相等 |
如果一个多边形的每一个外角都是60°,那么这个多边形是( )
| A、四边形 | B、五边形 |
| C、六边形 | D、八边形 |
 如图,在?ABCD中,BD=CD,∠C=70°,AE⊥BD于点E,则∠BAE的度数为( )
如图,在?ABCD中,BD=CD,∠C=70°,AE⊥BD于点E,则∠BAE的度数为( )| A、20° | B、30° |
| C、40° | D、50° |
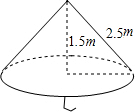 一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5m,高为1.5m,则做这把遮阳伞需用布料的面积(不计接缝)是( )
一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5m,高为1.5m,则做这把遮阳伞需用布料的面积(不计接缝)是( )| A、3πm2 | ||
| B、4πm2 | ||
| C、5πm2 | ||
D、
|
 如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个人球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是
如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个人球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是