Question

【题目】如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE， 交 AC于点F.

(1)如图①，当时，求的值；

(2)如图②当DE平分∠CDB时，求证：AF=OA；

(3)如图③，当点E是BC的中点时，过点F作FG⊥BC于点G，求证：CG=BG.

Answer 1

【答案】（1）；（2）（3）见解析

【解析】试题分析：（1）利用相似三角形的性质求得与的比值，依据和同高，则面积的比就是与的比值，据此即可求解；
（2）利用三角形的外角和定理证得 可以证得，在直角中，利用勾股定理可以证得；
（3）连接 易证是的中位线，然后根据是等腰直角三角形，易证 利用相似三角形的对应边的比相等即可．

试题解析：(1)∵，∴

∵四边形ABCD是正方形，

∴△CEF∽△ADF，∴，∴，∴；

(2)证明：∵DE平分∠CDB,

∴∠ODF=∠CDF，

∵AC、BD是正方形ABCD的对角线。

而∠ADF=∠ADO+∠ODF，∠AFD=∠FCD+∠CDF，

∴∠ADF=∠AFD，

∴AD=AF，

在中,根据勾股定理得：

AD==OA，

(3)证明：连接OE.

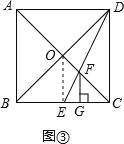
∵点O是正方形ABCD的对角线AC、BD的交点，

点O是BD的中点。

又∵点E是BC的中点，

∴OE是△BCD的中位线，

∴=，∴.

.在 中，∵∠GCF=45°.∴CG=GF，

又∵CD=BC，∴，

∴=.

∴CG=BG.