题目内容
 23、探索规律,由※组成的图案和算式,解答问题:
23、探索规律,由※组成的图案和算式,解答问题:1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请猜想1+3+5+7+9+…+19=
102
;(2)请猜想1+3+5+7+9+…+(2n-1)=
n2
.分析:由1+3=22;1+3+5=32;1+3+5+7=16=42;1+3+5+7+9=25=52,由此可以得出从1开始连续的奇数的和为相加的项数的平方.
解答:解:由图案1,3,5,7,9是连续的几个奇数;
由算式:1+3=22,从1开始连续2项奇数和;
1+3+5=32,从1开始连续3项奇数和;
1+3+5+7=16=42,从1开始连续4项奇数和;
1+3+5+7+9=25=52,从1开始连续5项奇数和;
可以得出规律:从1开始连续n个奇数的和等于n2,
所以:(1)1+3+5+7+9+…+19=102,从1开始连续10个奇数相加;
(2)1+3+5+7+9+…+(2n-1)=n2,从1开始n个奇数相加.
由算式:1+3=22,从1开始连续2项奇数和;
1+3+5=32,从1开始连续3项奇数和;
1+3+5+7=16=42,从1开始连续4项奇数和;
1+3+5+7+9=25=52,从1开始连续5项奇数和;
可以得出规律:从1开始连续n个奇数的和等于n2,
所以:(1)1+3+5+7+9+…+19=102,从1开始连续10个奇数相加;
(2)1+3+5+7+9+…+(2n-1)=n2,从1开始n个奇数相加.
点评:本题是规律型试题,关键在于发现从1开始连续n个奇数的和等于n2,这条规律,考查由给定图案和算式推出规律的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
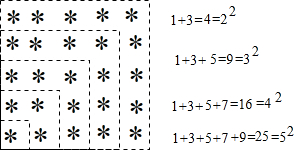 探索规律
探索规律 32、探索规律:观察下面由※组成的图案和算式,解答问题:
32、探索规律:观察下面由※组成的图案和算式,解答问题: 探索规律,由※组成的图案和算式,解答问题:
探索规律,由※组成的图案和算式,解答问题: