题目内容
【题目】如图,我东海舰队的一艘军舰在海面A处巡逻时发现一艘不明国籍的船只在C处游弋,立即通知在B处的另一艘军舰一起向其包抄,此时B在A的南偏西30°方向,我两艘军舰分别测得C在A的南偏东75°方向和C在B的北偏东75°方向,已知A,B之间的距离是30海里,求此刻我两艘军舰所在地A,B与C的距离.(结果保留根号)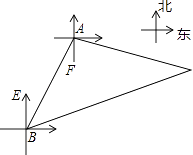
【答案】解:作AD⊥BC于D,如图,

∵AF∥BE,∠FAB=30°,∠EBC=75°,
∴∠EBA=∠FAB=30°,
∴∠ABC=∠EBC﹣∠EBA=45°,
又∵∠FAC=75°,
∴∠BAC=∠FAB+∠FAC=105°,
∴∠C=180°﹣∠ABC﹣∠BAC=30°,
在Rt△ABD中,
∵∠ABC=45°,AB=30海里,
∴AD= ![]() AB=15
AB=15 ![]() ,BD=AD=15
,BD=AD=15 ![]() ,
,
在Rt△ADC中,∵∠C=30°,
∴CD= ![]() AD=15
AD=15 ![]() ,AC=2AD=30
,AC=2AD=30 ![]() ,
,
∴BC=BD+CD=15 ![]() +15
+15 ![]() .
.
答:我两艘军舰所在地A、B与C的距离分别为30 ![]() 海里、(15
海里、(15 ![]() +15
+15 ![]() )海里.
)海里.
【解析】作AD⊥BC于D,由两直线平行,内错角相等得∠EBA=∠FAB=30°,由已知条件并结合角的运算得∠ABC=45°,∠BAC=105°,再由三角形的内角和定理得∠C=30°;在等腰Rt△ABD中,由勾股定理得BD=AD=15![]() ;在Rt△ADC中,由勾股定理求出CD=
;在Rt△ADC中,由勾股定理求出CD=![]() AD=15
AD=15![]() ,再由BC=BD+CD即可得出答案.
,再由BC=BD+CD即可得出答案.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目