题目内容
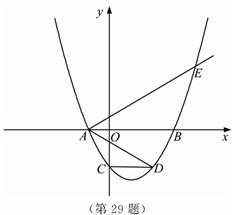
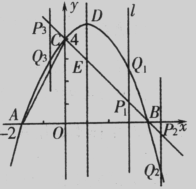
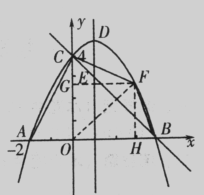
如图,抛物线y=ax2+bx+c(a≠O)与y轴交于点C(O,4),与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线Z 与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。
与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。

解:(1)由抛物 线经过点C(O,4)可得c=4,①
线经过点C(O,4)可得c=4,①
∵对称轴x=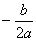 =1,∴b=-2a,②,
=1,∴b=-2a,②,
又抛物线过点A(一2,O)∴0=4a-2b+c,③
由①②③ 解得:a=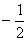 , b=1 ,c=4.
, b=1 ,c=4.
所以抛物线的解析式是y=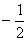 x+x+4
x+x+4
(2)假设存在满足条件的点F,如图如示,连接BF、CF、OF.
过点F分别作FH⊥x轴于H , FG⊥y轴于G.
设点F的坐标为(t, 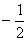 t2+t+4),
t2+t+4), 其中O<t<4,
其中O<t<4,
则FH= t2 +t+4 FG=t,
t2 +t+4 FG=t,
∴△OBF=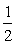 OB.FH=
OB.FH=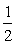 ×4×(
×4×( t2+4t+4)=一t2+2t+8
t2+4t+4)=一t2+2t+8
S△OFC=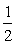 OC.FC=
OC.FC=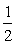 ×4×t=2t
×4×t=2t
∴S四边形ABFC—S△AOC+S△OBF +S△OFC=4-t2+2t+8+2t=-t2+4t+12.
令一t2+4t+12 =17,即t2-4t+5=0,则△=(一4)2-4×5=一4<0,
∴方程t2 -4t+5=0无解,故不存在满足条件的点F..
 (3)设直线BC的解析式为y=kx+b(k≠O),又过点B(4,0,), C(0,4)
(3)设直线BC的解析式为y=kx+b(k≠O),又过点B(4,0,), C(0,4)
所以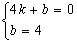 ,解得:
,解得: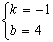 ,
,
所以直线BC的解析式是y=一x+4. .
由y= x2+4x+4=一
x2+4x+4=一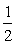 (x一1)2+
(x一1)2+ ,得D(1,
,得D(1, ), .
), .
又点E在直线BC上,则点E(1,3),
于是DE= 一3=
一3= 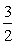

若以D.E.P.Q为顶点的四边形是平行四边形,因为DE∥PQ,只须DE=PQ,
设点P的坐标是(m,一m+4),则点Q的坐标是(m,一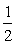 t2+m+4).
t2+m+4).
①当O<m<4时,PQ=(一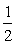 t2+m+4)一(一m+4)=一
t2+m+4)一(一m+4)=一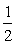 m2+2m.
m2+2m.
由一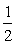 m2+2m=
m2+2m=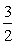 ,解得:m=1或3.当m=1时,线段PQ与DE重合,m=-1舍去,
,解得:m=1或3.当m=1时,线段PQ与DE重合,m=-1舍去,
∴m=-3,此时P1 (3,1).
②当m<o或m>4时,PQ=(一m+4)一(一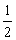 m2++m+4)=
m2++m+4)= 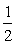 m2—2m,
m2—2m,
由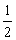 m2—2m=
m2—2m=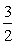 ,解得m=2±
,解得m=2±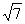 ,经检验适合题意,
,经检验适合题意,
此时P2(2+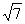 ,2一
,2一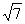 ),P3(2一
),P3(2一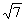 ,2+
,2+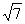 ).
).
综上所述,满足条件的点P有三个,分别是P1 (3,1),P2(2+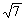 ,2 -
,2 -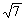 ),P3(2—
),P3(2—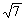 ,2十
,2十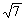 ).
).

 优生乐园系列答案
优生乐园系列答案 的立方根是 _________ .
的立方根是 _________ .
 _________
_________ .
. 
 B.
B. C.
C. D.
D.

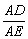 为定值;
为定值; 三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数
三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数 式表示该点的横坐标;如果不存在,请说明理由.
式表示该点的横坐标;如果不存在,请说明理由.