题目内容
【题目】给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
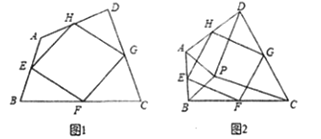
(1)如图1,四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,
,![]() 分别为边
分别为边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,则中点四边形
的中点,则中点四边形![]() 形状是_______________.
形状是_______________.
(2)如图2,点![]() 是四边形
是四边形![]() 内一点,且满足
内一点,且满足![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 分别为边
分别为边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,求证:中点四边形
的中点,求证:中点四边形![]() 是正方形.
是正方形.
【答案】(1) 平行四边形;(2)见解析
【解析】
(1)如图1中,连接BD,根据三角形中位线定理只要证明EH∥FG,EH=FG即可.
(2)首先证明四边形EFGH是菱形.再证明∠EHG=90°.利用△APC≌△BPD,得∠ACP=∠BDP,即可证明∠COD=∠CPD=90°,再根据平行线的性质即可证明.
(1)证明:如图1中,连接BD.
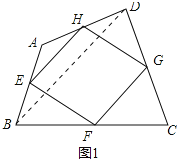
∵点E,H分别为边AB,DA的中点,
∴EH∥BD,EH=![]() BD,
BD,
∵点F,G分别为边BC,CD的中点,
∴FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=GF,
∴中点四边形EFGH是平行四边形.
故答案为平行四边形;
(2)证明:如图2中,连接![]() ,
,![]() .
.
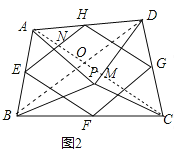
∵![]() ,∴
,∴![]() 即
即![]() ,
,
在![]() 和
和![]() 中,
中,
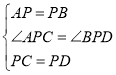 ,
,
∴![]() ,
,
∴![]()
∵点![]() ,
,![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
由(1)可知,四边形![]() 是平行四边形,
是平行四边形,
∴四边形![]() 是菱形.
是菱形.
如图设![]() 与
与![]() 交于点
交于点![]() .
.![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴四边形![]() 是正方形.
是正方形.

练习册系列答案
相关题目