Question

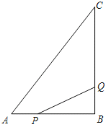
【题目】如图，AB与⊙O相切于点C，OA=OB，⊙O的直径为6 cm，AB=6 cm，则阴影部分的面积为（ ）

A. B.

C. D.

Answer 1

【答案】C

【解析】

如图，连接OC，由切线的性质可得∠ACO=90°，根据OA=OB，AB=6，可得AC=3，∠A=∠B，在Rt△AOC中，可求得∠A=30°，继而可得∠AOB=120°，根据S阴影=S△AOB-S扇形ODE进行计算即可得.

如图，连接OC，则OC==3，

∵AB与⊙O相切于点C，

∴OC⊥AB，即∠ACO=90°，

∵OA=OB，AB=6，

∴AC=AB=3，∠A=∠B，

在Rt△AOC中，tan∠A=，

∴∠A=30°，

∴∠AOB=180°-∠A-∠B=120°，

∴S阴影=S△AOB-S扇形ODE== ，

故选C.