题目内容
 在△ABC中,DE是中位线,∠B的平分线交DE于F,则△ABF一定是
在△ABC中,DE是中位线,∠B的平分线交DE于F,则△ABF一定是
- A.锐角三角形
- B.直角三角形
- C.钝角三角形
- D.直角三角形或钝角三角形
B
分析:根据角平分线的性质及中位线定理可得BD=BF,再根据如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形即可得到答案.
解答:∵∠B的平分线交DE于F.
∴∠DBF=∠FBC.
∵DE是中位线.
∴DE∥BC.
∴∠DFB=∠FBC.
∴∠DBF=∠DFB.
∴BD=BF.
∵DE是中位线.
∴AD=DB.
∴DF= AB.
AB.
∴△ABF一定是直角三角形.
故选B.
点评:此题主要考查:
(1)三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
(2)直角三角形斜边上的中线的定理:一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.
分析:根据角平分线的性质及中位线定理可得BD=BF,再根据如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形即可得到答案.
解答:∵∠B的平分线交DE于F.
∴∠DBF=∠FBC.
∵DE是中位线.
∴DE∥BC.
∴∠DFB=∠FBC.
∴∠DBF=∠DFB.
∴BD=BF.
∵DE是中位线.
∴AD=DB.
∴DF=
 AB.
AB.∴△ABF一定是直角三角形.
故选B.
点评:此题主要考查:
(1)三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
(2)直角三角形斜边上的中线的定理:一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.

练习册系列答案
相关题目
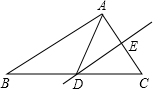 如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是
如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是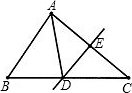 如图,在△ABC中,DE是AC的垂直平分线,△ABC和△ABD的周长分别为18cm和12cm.则线段AE为
如图,在△ABC中,DE是AC的垂直平分线,△ABC和△ABD的周长分别为18cm和12cm.则线段AE为 如图,在△ABC中,DE是边AB的垂直平分线,其中∠B=40°,∠EAC=35°,则∠C=
如图,在△ABC中,DE是边AB的垂直平分线,其中∠B=40°,∠EAC=35°,则∠C= 如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为17cm,求△ABC的周长.
如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为17cm,求△ABC的周长. 如图所示,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.
如图所示,在△ABC中,DE是边AB的垂直平分线,交AB于E,交AC于D,连接BD.