题目内容
已知:直线AB与直线CD相交于点O,∠BOC=45°.

(1)如图1,若EO⊥AB,求∠DOE的度数;
(2)如图2,若FO平分∠AOC,求∠DOF的度数.
【答案】
(1)135°;(2)112.5°.
【解析】
试题分析:(1)根据对顶角的性质可得∠AOD=∠BOC=45°,再根据垂直定义可得∠AOE=90°,再利用角的和差关系可得答案;
(2)首先根据邻补角定义可得∠AOC=135°,再根据角平分线的性质可得∠AOF的度数,然后再利用角的和差关系求出∠DOF的度数.
试题解析:(1)∵直线AB与直线CD相交于O,
∴∠AOD=∠BOC=45°,
∵EO⊥AB,
∴∠AOE=90°,
∴∠DOE=∠AOD+∠AOE=135°;
(2)∵∠BOC=45°,
∴∠AOC=135°,
∵FO平分∠AOC,
∴∠AOF=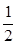 ∠AOC=67.5°,
∠AOC=67.5°,
∠DOF=∠AOD+∠AOF=112.5°.
考点: 垂线;对顶角、邻补角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
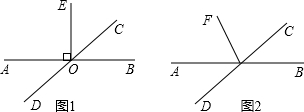 已知:直线AB与直线CD相交于点O,∠BOC=45°.
已知:直线AB与直线CD相交于点O,∠BOC=45°.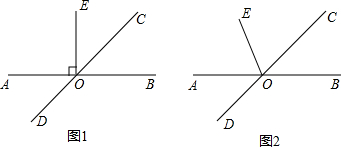 已知:直线AB与直线CD相交于点O,∠BOC=45°,
已知:直线AB与直线CD相交于点O,∠BOC=45°, ,
, ),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
 ,
, ),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
 ,
, ),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
),B点在y轴上,直线与x轴的交点为F,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.