题目内容
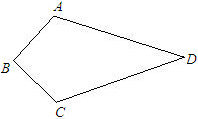
已知如图，四边形ABCD中，AB=BC，∠A=∠C，求证：AD=CD．
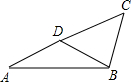
证明：连接AC，
∵△ABC中，AB=BC，
∴∠BCA=∠BAC．
又∵∠BAD=∠BCD，∠BCD=∠BCA+∠ACD，∠BAD=∠BAC+∠CAD；
∴∠CAD=∠ACD．
∴AD=CD（等角对等边）．
∵△ABC中，AB=BC，
∴∠BCA=∠BAC．
又∵∠BAD=∠BCD，∠BCD=∠BCA+∠ACD，∠BAD=∠BAC+∠CAD；
∴∠CAD=∠ACD．
∴AD=CD（等角对等边）．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
