题目内容
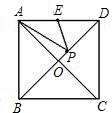如图，P是边长为4的正方形ABCD的对角线BD上的一动点，且点E是边AD的中点，求PE+PA的最小值为________．
2
分析：由于点A与点C关于BD对称，所以如果连接EC，交BD于点P，那PE+PA的值最小．在Rt△CDE中，由勾股定理先计算出EC的长度，即为PE+PA的最小值．
解答：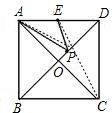
解：连接EC，交BD于点P，连接PA．
∵点A与点C关于BD对称，
∴AP=CP，
∴PE+PA=PE+PC=EC．
在Rt△CDE中，EC=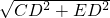
=
=2．
故答案为：2．
点评：本题考查了轴对称-最短路线问题和正方形的性质，根据两点之间线段最短，可确定点P的位置．
分析：由于点A与点C关于BD对称，所以如果连接EC，交BD于点P，那PE+PA的值最小．在Rt△CDE中，由勾股定理先计算出EC的长度，即为PE+PA的最小值．
解答：
解：连接EC，交BD于点P，连接PA．∵点A与点C关于BD对称，
∴AP=CP，
∴PE+PA=PE+PC=EC．
在Rt△CDE中，EC=
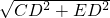==2．故答案为：2
．点评：本题考查了轴对称-最短路线问题和正方形的性质，根据两点之间线段最短，可确定点P的位置．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
14、如图，O是边长为6的等边三角形ABC内的任意一点，且OD∥BC，交AB于点D，OF∥AB，交AC于F，OE∥AC，交BC于E．则OD+OE+OF的值（ ）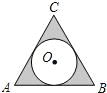
如图，⊙O是边长为2的等边三角形ABC的内切圆，则图中阴影部分的面积为
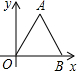如图，△AOB是边长为5的等边三角形，则A，B两点的坐标分别是A
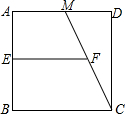如图，M是边长为2cm的正方形ABCD的边AD的中点，E、F分别是AB、CM的中点．则EF=
如图，△ABC是边长为6的等边三角形，AD=2，AE∥BC，直线BD交AE于点E，则BE的长为（ ）