题目内容
 已知如图:⊙O中,BC是直径,点A在⊙O上,AB=6,AC=8,AD平分∠BAC
已知如图:⊙O中,BC是直径,点A在⊙O上,AB=6,AC=8,AD平分∠BAC
(1)求BC的长;
(2)求BD的长.
 解:(1)∵BC是⊙O的直径,
解:(1)∵BC是⊙O的直径,∴∠BAC=90°,
∵AB=6,AC=8,
∴BC=
 =
= =10;
=10;(2)连接OD,
∵AD平分∠BAC,∠BAC=90°,
∴∠BAD=45°,
∴∠BOD=2∠BAD=90°,
∵OB=OD=
 BC=
BC= ×10=5,
×10=5,∴BD=
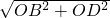 =
=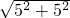 =5
=5 .
.分析:(1)先根据圆周角定理求出∠BAC的度数,再由勾股定理即可得出BC的长;
(2)连接OD,由圆周角定理得出∠BOD的度数,再根据勾股定理即可求出BD的长.
点评:本题考查的是圆周角定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
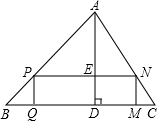 已知如图,△ABC中BC=60cm,高AD=40cm,四边形PQMN是矩形,点P在AB边上,点Q、M在BC边上,点N在AC边上.
已知如图,△ABC中BC=60cm,高AD=40cm,四边形PQMN是矩形,点P在AB边上,点Q、M在BC边上,点N在AC边上. 已知如图,△ABC中,AB>AC,AD是高,AE是角平分线,试说明
已知如图,△ABC中,AB>AC,AD是高,AE是角平分线,试说明 已知如图,⊙O中,AE为直径,AD⊥BC
已知如图,⊙O中,AE为直径,AD⊥BC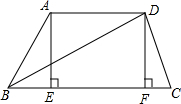 已知如图梯形ABCD中,AD∥BC,∠ABC=60°,BD=2
已知如图梯形ABCD中,AD∥BC,∠ABC=60°,BD=2 已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )
已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )