题目内容
(2011•自贡)阅读下面例题的解答过程,体会、理解其方法,并借鉴该例题的解法解方程.
例:解方程x2-|x-1|-1=0
解:(1)当x-1≥0即x≥1时.|x-1|=x-1,
原方程化为x2-(x-1)-1=0,即x2-x=0,
解得x1=0,x2=1.
∵x≥1,故x=0舍去,x=1是原方程的解
(2)当x-1<0即x<1时.|x-1|=-(x-1),
原方程化为x2+(x-1)-1=0,即x2+x-2=0,
解得x1=1,x2=-2.
∵x<1,故x=1舍去,x=-2是原方程的解.
综上所述,原方程的解为x1=1,x2=-2.
解方程:x2+2|x+2|-4=0.
例:解方程x2-|x-1|-1=0
解:(1)当x-1≥0即x≥1时.|x-1|=x-1,
原方程化为x2-(x-1)-1=0,即x2-x=0,
解得x1=0,x2=1.
∵x≥1,故x=0舍去,x=1是原方程的解
(2)当x-1<0即x<1时.|x-1|=-(x-1),
原方程化为x2+(x-1)-1=0,即x2+x-2=0,
解得x1=1,x2=-2.
∵x<1,故x=1舍去,x=-2是原方程的解.
综上所述,原方程的解为x1=1,x2=-2.
解方程:x2+2|x+2|-4=0.
分析:由于x+2的符号不能确定,故应分x+2≥0和x+2<0两种情况,结合绝对值的性质去掉绝对值符号,再解关于x的一元二次方程即可.
解答:解:(1)当x+2≥0即x≥-2时.|x+2|=x+2,
原方程化为x2+2(x+2)-4=0,即x2+2x=0,
解得x1=0,x2=-2.
∵x≥-2,
故x1=0,x2=-2是原方程的解;
(2)当x+2<0即x<-2时.|x+2|=-(x+2),
原方程化为x2-2(x+2)-4=0,即x2-2x-8=0,
解得x1=4,x2=-2.
∵x<-2,
故x1=0,x2=-2(不是原方程的解,舍去)
综上所述,原方程的解为x=0.
原方程化为x2+2(x+2)-4=0,即x2+2x=0,
解得x1=0,x2=-2.
∵x≥-2,
故x1=0,x2=-2是原方程的解;
(2)当x+2<0即x<-2时.|x+2|=-(x+2),
原方程化为x2-2(x+2)-4=0,即x2-2x-8=0,
解得x1=4,x2=-2.
∵x<-2,
故x1=0,x2=-2(不是原方程的解,舍去)
综上所述,原方程的解为x=0.
点评:本题考查的是含绝对值符号的一元二次方程,在解答此类题目时一定要注意分类讨论.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 (2011•自贡)如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有
(2011•自贡)如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有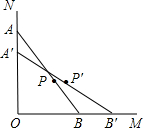 (2011•自贡)如图,一根木棒(AB)长为2a,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿N0向下滑动到A′,AA′=
(2011•自贡)如图,一根木棒(AB)长为2a,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿N0向下滑动到A′,AA′=