题目内容
已知x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根,则使 的值为整数的实数k的整数值为________.
的值为整数的实数k的整数值为________.
-5,-3,-2,0,1,3
分析:由x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根,利用根与系数的关系表示出x1+x2与x1x2,将 +
+ -2通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出x1+x2与x1x2代入,整理后根据此式子的值为整数,即可求出实数k的整数值.
-2通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出x1+x2与x1x2代入,整理后根据此式子的值为整数,即可求出实数k的整数值.
解答:∵x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根,
∴x1+x2=1,x1x2= ,
,
∴ +
+ -2=
-2=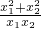 -2=
-2= -2=
-2= -2=
-2= -2=
-2= ,
,
由此式子的值为整数,得到k=-5,-3,-2,0,1,3.
故答案为:-5,-3,-2,0,1,3
点评:此题考查了一元二次方程根与系数的关系,熟练掌握根与系数的关系是解本题的关键.
分析:由x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根,利用根与系数的关系表示出x1+x2与x1x2,将
 +
+ -2通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出x1+x2与x1x2代入,整理后根据此式子的值为整数,即可求出实数k的整数值.
-2通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出x1+x2与x1x2代入,整理后根据此式子的值为整数,即可求出实数k的整数值.解答:∵x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根,
∴x1+x2=1,x1x2=
 ,
,∴
 +
+ -2=
-2=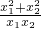 -2=
-2= -2=
-2= -2=
-2= -2=
-2= ,
,由此式子的值为整数,得到k=-5,-3,-2,0,1,3.
故答案为:-5,-3,-2,0,1,3
点评:此题考查了一元二次方程根与系数的关系,熟练掌握根与系数的关系是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x1、x2是一元二次方程ax2+bx+c=0的两根,且判别式△=b2-4ac≥0,则x1-x2的值为( )
A、
| ||||
B、
| ||||
C、±
| ||||
D、±
|