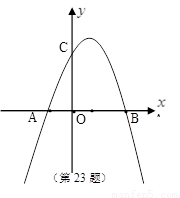题目内容
如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过
,且经过![]() 两点,点
两点,点![]() 是抛物线顶点,
是抛物线顶点,![]() 是对称轴与直线
是对称轴与直线![]() 的交点,
的交点,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
(1)求抛物线的解析式;
(2)求证:![]() ;
;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似.若有,请求出所有符合条件的点
相似.若有,请求出所有符合条件的点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
 |
答案:解:(1)将点![]() 代入
代入![]() 得
得
![]() ……………………1分
……………………1分
解之得![]() ,
,
所以抛物线的解析式为![]() ………2分
………2分
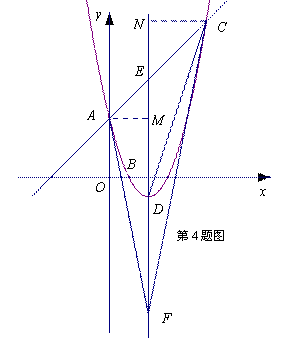
(2)由(1)可得抛物线顶点![]() …… 3分
…… 3分
直线![]() 的解析式为
的解析式为![]()
由![]() 是对称轴与直线
是对称轴与直线![]() 的交点,则
的交点,则![]()
由![]() 与
与![]() 关于点
关于点![]() 对称 ,则
对称 ,则![]() ………4分
………4分
证法一:
从点![]() 分别向对称轴作垂线
分别向对称轴作垂线![]() ,交对称轴于
,交对称轴于![]()
在![]() 和
和![]() 中
中
![]() ,
,![]()
所以![]() ∽
∽![]()
所以![]() …………………………………5分
…………………………………5分
证法二:直线![]() 的解析式为
的解析式为![]()
点 ![]() 关于对称轴的对称点是
关于对称轴的对称点是![]()
将点![]() 代入
代入![]() 可知点
可知点![]() 在直线
在直线![]()
所以![]()
(3)在![]() 中,三内角不等,且
中,三内角不等,且![]() 为钝角
为钝角
① 若点![]() 在点
在点![]() 下方时,
下方时,
在![]() 中,
中,![]() 为钝角
为钝角
因为![]() ,
,![]()
所以![]() 和
和![]() 不相等
不相等
所以,点![]() 在点
在点![]() 下方时,两三角形不能相似 …………………… 6分
下方时,两三角形不能相似 …………………… 6分
② 若点![]() 在点
在点![]() 上方时,
上方时,
由![]() ,要使
,要使![]() 与
与![]() 相似
相似
只需![]() (点
(点![]() 在
在![]() 之间)或
之间)或![]() (点
(点![]() 在
在![]() 的延长线上)
的延长线上)
解得点![]() 的坐标为
的坐标为![]() 或
或![]() ………………………………………8分
………………………………………8分

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
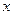 轴交于点
轴交于点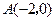 ,
,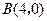 ,与
,与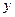 轴交于点
轴交于点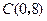 .
.
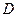 的坐标;
的坐标;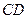 交
交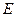 .在线段
.在线段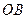 的垂直平分线上是否存在点
的垂直平分线上是否存在点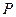 ,使得点
,使得点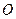 的距离?如果存在,求出点
的距离?如果存在,求出点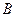 作
作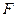 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段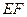 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?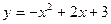 与
与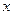 轴的两个交点为A、B,与
轴的两个交点为A、B,与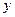 轴交于点C
轴交于点C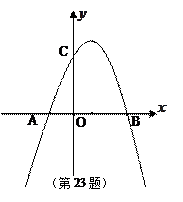
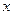 轴交于点
轴交于点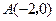 ,
,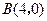 ,与y轴交于点
,与y轴交于点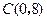 .
.

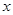 轴交于点
轴交于点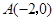 ,
,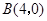 ,与y轴交于点
,与y轴交于点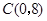 .
.
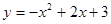 与
与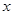 轴的两个交点为A、B,与
轴的两个交点为A、B,与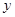 轴交于点C
轴交于点C