Question

【题目】(1)问题发现

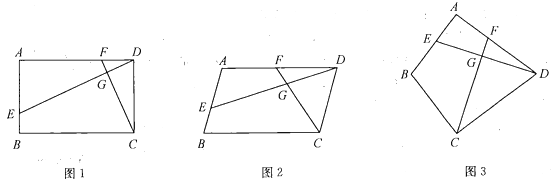
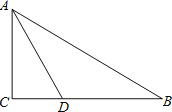
如图， 在和中，，，， 连接，交于点．填空：①的值为 ：②的度数为

(2)类比探究

如图， 在和中，，， 连接交的延长线于点．请求出能的值及的度数， 并说明理由；

(3)拓展延伸

在的条件下， 将绕点在平面内旋转，所在直线交于点， 若，，请直接写出当点与点重合时的长．

Answer 1

【答案】（1）；（2）．理由见解析（3）的长为或．

【解析】

（1）①证明，得到AC=BD，比值为1；②由得，根据三角形内角和定理得，=．

（2）根据两边的比相等且夹角相等可得∽，则，由全等三角形的性质得的度数．

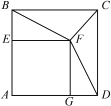
（3）正确画出图形，当点C与点M重合时，有两种情况：如图3和如图4，同理可得，则，，可得AC的长．

（1）；

①如图1.

∵,

∴，

∵OC=OD，OA=OB，

∴，

∴AC=BD，

∴．

②∵，

∴，

∵，

∴，

在，

，

=，

=，

故答案为：1，．

（2）．理由如下：

在，中

∴，同理可得

∴

∵

∴

∴∽

∴

∴

（3）拓展延伸

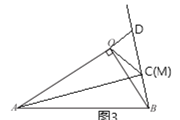
①点C与点M重合时，如图3，同理得：，

∴，，

设，则，

Rt△COD中，，OD=1，

∴，,

Rt△AOB中，，，

∴，

在RtAMB中，由勾股定理得：

，

，

，

解得：，，

∴；

②点C与点M重合时，如图4，

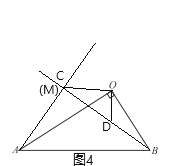
同理得：，，

设，则，

在RtAMB中，由勾股定理得：

，

，

，

解得：，，

∴

综上所述：的长为或．