Question

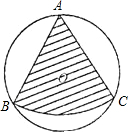
如图，圆（直径为）的切点分别为A，B，C，那么图中的距离x=    ．（用最简分数表示）．

Answer 1

【答案】分析：∵与⊙O相切于C点的直线∥EF，△GEF是等边三角形，由等边三角形的性质与圆的切线的性质通过作辅助线和运用勾股定理就可以GB的值，用含x的式子表示出HF、OF的值，在Rt△OBF中由勾股定理建立等量关系就可以求出x的值．
解答：解：连接CO、OG、OF、OB，CO交EF于点H．
∵⊙O的直径是
∴OC=OB=，GH=，HC=x
∴OH=-x
∵△GEF是等边三角形
∴∠OGF=30°
∴GF=2HF
在Rt△GHF中，由勾股定理，得
HF=，GF=，
在Rt△HOF中，由勾股定理，得
OF²=
在Rt△OBG中，由勾股定理，得
GB=，BF=-
在Rt△OBF中，由勾股定理，得
-=，
解得：x₁=（不符合题意，舍去），x₂=．
故答案为：．
点评：本题考查了圆的切线的性质，等边三角形的性质，勾股定理的运用等知识点，是一道计算量较大试题．