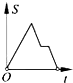题目内容
13.已知反比例函数y=$\frac{1-6t}{x}(t≠\frac{1}{6})$,如果在这个函数图象所在的每一个象限内,y的值随着x的值增大而减小,那么t的取值范围是t<$\frac{1}{6}$.分析 根据反比例函数性质:函数图象所在的每一个象限内,y的值随着x的值增大而减小,则比例系数1-6t>0,据此求得t.
解答 解:根据题意得1-6t>0,
解得t<$\frac{1}{6}$.
故答案是:t<$\frac{1}{6}$.
点评 本题考查了反比例函数的性质,反比例函数y=$\frac{k}{x}$,当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小,当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
5.2016年普宁市重点项目累计完成投资187.35亿元,将187.35亿用科学记数法表示为( )
| A. | 187.35×108 | B. | 1.8735×109 | C. | 1.8735×1010 | D. | 1.8735×1011 |
4.某一天,水果经营户老刘从水果批发市场批发苹果和芒果共40kg到市场去卖,已知苹果和芒果当天的批发价和零售价如表所示:
(1)如果当天他卖完这些苹果和芒果共获利60元,这天他批发的苹果和芒果分别是多少千克?
(2)假设老刘带了150元去水果批发市场批发苹果和芒果,并且当天都能卖完所批水果,老刘该如何进货,才能使得所获利润最大?最大利润是多少?
| 品名 | 苹果 | 芒果 |
| 批发价(元/kg) | 3 | 4 |
| 零售价(元/kg) | 4 | 7 |
(2)假设老刘带了150元去水果批发市场批发苹果和芒果,并且当天都能卖完所批水果,老刘该如何进货,才能使得所获利润最大?最大利润是多少?
5.下面四个图形中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
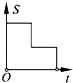
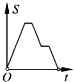
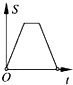
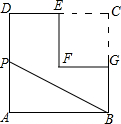 如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )