题目内容
 如图,?ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合,若△ACD的面积为3,则图中阴影部分两个三角形的面积和为( )
如图,?ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合,若△ACD的面积为3,则图中阴影部分两个三角形的面积和为( )| A、6 | B、3 | C、2 | D、1 |
考点:矩形的性质,平行四边形的性质
专题:
分析:根据平行四边形的对角线把平行四边形分成的两个三角形的面积相等求出△ABC的面积,再根据三角形的面积公式和矩形的面积公式求出矩形的面积,然后求解即可.
解答:解:在?ABCD中,∵△ACD的面积为3,
∴△ABC的面积为3,
∴S△ABC=
AC•AE=3,
∴AC•AE=3×2=6,
∴矩形AEFC的面积为6,
阴影部分两个三角形的面积和=6-3=3.
故选B.
∴△ABC的面积为3,
∴S△ABC=
| 1 |
| 2 |
∴AC•AE=3×2=6,
∴矩形AEFC的面积为6,
阴影部分两个三角形的面积和=6-3=3.
故选B.
点评:本题考查了矩形的性质,平行四边形的性质,根据三角形的面积求出矩形的面积是解题的关键,也是本题的难点.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 在宽为20m,长为32m的矩形田地中央修筑同样宽的两条互相垂直的道路,把矩形田地分成四个相同面积的小田地,作为良种试验田,要使每小块试验田的面积为135m2,则道路的宽为( )
在宽为20m,长为32m的矩形田地中央修筑同样宽的两条互相垂直的道路,把矩形田地分成四个相同面积的小田地,作为良种试验田,要使每小块试验田的面积为135m2,则道路的宽为( )| A、50m | B、5m | C、2m | D、1m |
计算4x3÷x2的结果是( )
| A、3x2 |
| B、4x2 |
| C、4x |
| D、4 |
重庆市园博园准备选购500棵高度大约为2米的树苗来进行绿化,有四个苗圃基地投标(单株树的价格相同),采购小组从四个苗圃中任意抽查了20株树苗的高度,得到下表中的数据:
你认为应选( )
| 甲苗圃 | 乙苗圃 | 丙苗圃 | 丁苗圃 | |
| 树苗的平均高度(米) | 1.8 | 1.8 | 2.0 | 2.0 |
| 标准差 | 0.2 | 0.4 | 0.2 | 0.4 |
| A、甲苗圃的树苗 |
| B、乙苗圃的树苗 |
| C、丙苗圃的树苗 |
| D、丁苗圃的树苗 |
已知(x-2)x+3=1,则x的值为( )
| A、3 | B、-2 |
| C、3或-2 | D、3或-3或1 |
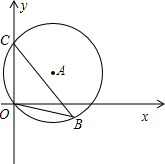 如图,直径为10的⊙A经过点C(0,5)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为( )
如图,直径为10的⊙A经过点C(0,5)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为( )