题目内容
已知抛物线y=ax2+c的顶点为D(0,![]() ),且过点A(1,
),且过点A(1,![]() ),如图所示.
),如图所示.

(1)试求这条抛物线的代数表达式;
(2)点F是坐标原点O关于该抛物线顶点D的对称点,坐标为(0,![]() ),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴,过F作x轴的平行线交AA1于点A2,则FA2=1,A2A=
),我们可以用以下方法求线段FA的长度:过点A作AA1⊥x轴,过F作x轴的平行线交AA1于点A2,则FA2=1,A2A=![]() -
-![]() =
=![]() .在Rt△AFA2中,有FA=
.在Rt△AFA2中,有FA=![]() =
=![]() .
.
已知抛物线上另一点B的横坐标为2,求线段FB的长.
(3)若点P是该抛物线上在第一象限内的任意一点,试探究线段FP的长度与点P的纵坐标的大小关系,并证明你的猜想.
答案:
解析:
提示:
解析:
|
[答案](1)由已知,得
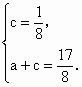 解这个方程组,得 解这个方程组,得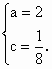
∴该抛物线的代数表达式为y=2x2+ (2)当x=2时,y=2×22+ 即点 B的坐标为(2,如图,过 B作BB1⊥x轴于点B1,过F作FB2∥x轴交BB1于点B2,则FB2=2,BB2=在 Rt△BFB2中,FB=(3)相等 设 P点的坐标为(x,y),则x>0,y>0,且y=2x2+过 P作PP1⊥x轴于P1,过F作FP2∥x轴交PP1于点P2,则FP2=x,PP2=y-在 Rt△PFP2中,FP=∴抛物线在第一象限内的任意一点P到点F的距离等于这一点P的纵坐标. [剖析]由FA、FB的长,可获得第(3)问的猜想,从FA、FB的长的求解过程可发现,求长的关键是要知道该点的坐标,故可先设出P点坐标(由于P点在第一象限,故x>0,y>0,然后用x的代数式表示FP的长度,最后由y与x的关系获得FP与y的关系. |
提示:
|
[方法提炼] 通过阅读、理解,获得一种新的方法,然后运用新方法解决问题.另外还要注意从结论和过程两个角度进行归纳,以获得一般性的结论和解法. |

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.

 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;