题目内容
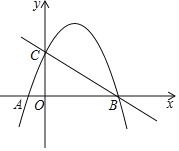
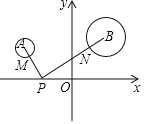
【题目】如图，平面直角坐标系中，分别以点A （﹣2，3），B（3，4）为圆心，以1、2为半径作⊙A、⊙B，M、N分别是⊙A、⊙B上的动点，P为x轴上的动点，则PM+PN的最小值等于（ ）
A.
B.+3C.﹣3D.3
【答案】C
【解析】
作⊙A关于x轴的对称⊙
，
交⊙于点M，连接
交⊙B于点N，交x轴于P，如图，根据两点之间线段最短得到此时PM+PN最小，再利用对称确定的坐标，接着利用两点间的距离公式计算出
的长，然后用的长减去两个圆的半径即可得到MN的长，从而得到PM+PN的最小值．
解：作⊙A关于x轴的对称⊙ ，交⊙于点M，连接交⊙B于点N，交x轴于P，则此时PM+PN最小，
∵点A坐标（﹣2，3），
∴点A′坐标（﹣2，﹣3），
∵点B（3，4），
∴
，
∴
，
∴PM+PN的最小值为
．
故选：C．
练习册系列答案
相关题目
【题目】某运输公司现将一批152吨的货物运往A，B两地，若用大小货车15辆，则恰好能一次性运完这批货．已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆，其运往A，B两地的运费如下表所示：
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆．(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地，其余货车前往B地，设前往A地的大货车为x辆，前往A，B两地总费用为w元，试求w与x的函数解析式．
