题目内容
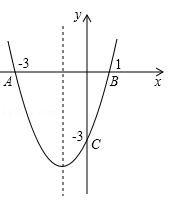
如图,抛物线l交x轴于点A(﹣3,0)、B(1,0),交y轴于点C(0,﹣3),将抛物线l沿y轴翻折得抛物线l1.
(1)求l1的解析式;
(2)在l1的对称轴上找出点P,使点P到点A的对称点A1及C两点的距离差最大,并说出理由;
(3)平行于x轴的一条直线交抛物线l1于E、F两点,若以EF为直径的圆恰与x轴相切,求此圆的半径
(1)求l1的解析式;
(2)在l1的对称轴上找出点P,使点P到点A的对称点A1及C两点的距离差最大,并说出理由;
(3)平行于x轴的一条直线交抛物线l1于E、F两点,若以EF为直径的圆恰与x轴相切,求此圆的半径
解:(1)如图1所示,设经翻折后,点A、B的对应点分别为A1、B1,
依题意,由翻折变换的性质可知A1(3,0),B1(﹣1,0),C点坐标不变,
因此,抛物线l1经过A1(3,0),B1(﹣1,0),C(0,﹣3)三点,设抛物线l1的解析式为y=ax2+bx+c,
则有: ,
,
解得a=1,b=﹣2,c=﹣3,
故抛物线l1的解析式为:y=x2﹣2x﹣3.
(2)抛物线l1的对称轴为:x= =1,
=1,
如图2所示,连接B1C并延长,与对称轴x=1交于点P,则点P即为所求.
此时,|PA1﹣PC|=|PB1﹣PC|=B1C.
设P'为对称轴x=1上不同于点P的任意一点,
则有:|P'A﹣P'C|=|P'B1﹣P'C|<B1C(三角形两边之差小于第三边),
故|P'A﹣P'C|<|PA1﹣PC|,即|PA1﹣PC|最大.
设直线B1C的解析式为y=kx+b,
则有: ,解得k=b=﹣3,
,解得k=b=﹣3,
故直线B1C的解析式为:y=﹣3x﹣3.
令x=1,得y=﹣6,
故P(1,﹣6).
(3)依题意画出图形,如图3所示,
有两种情况.
①当圆位于x轴上方时,设圆心为D,半径为r,
由抛物线及圆的对称性可知,点D位于对称轴x=1上,
则D(1,r),F(1+r,r).
∵点F(1+r,r)在抛物线y=x2﹣2x﹣3上,
∴r=(1+r)2﹣2(1+r)﹣3,
化简得:r2﹣r﹣4=0
解得r1= ,r2=
,r2= (舍去),
(舍去),
∴此圆的半径为 ;
;
②当圆位于x轴下方时,
同理可求得圆的半径为 .
.
综上所述,此圆的半径为 或
或
依题意,由翻折变换的性质可知A1(3,0),B1(﹣1,0),C点坐标不变,
因此,抛物线l1经过A1(3,0),B1(﹣1,0),C(0,﹣3)三点,设抛物线l1的解析式为y=ax2+bx+c,
则有:
 ,
,解得a=1,b=﹣2,c=﹣3,
故抛物线l1的解析式为:y=x2﹣2x﹣3.
(2)抛物线l1的对称轴为:x=
 =1,
=1,如图2所示,连接B1C并延长,与对称轴x=1交于点P,则点P即为所求.
此时,|PA1﹣PC|=|PB1﹣PC|=B1C.
设P'为对称轴x=1上不同于点P的任意一点,
则有:|P'A﹣P'C|=|P'B1﹣P'C|<B1C(三角形两边之差小于第三边),
故|P'A﹣P'C|<|PA1﹣PC|,即|PA1﹣PC|最大.
设直线B1C的解析式为y=kx+b,
则有:
 ,解得k=b=﹣3,
,解得k=b=﹣3,故直线B1C的解析式为:y=﹣3x﹣3.
令x=1,得y=﹣6,
故P(1,﹣6).
(3)依题意画出图形,如图3所示,
有两种情况.
①当圆位于x轴上方时,设圆心为D,半径为r,
由抛物线及圆的对称性可知,点D位于对称轴x=1上,
则D(1,r),F(1+r,r).
∵点F(1+r,r)在抛物线y=x2﹣2x﹣3上,
∴r=(1+r)2﹣2(1+r)﹣3,
化简得:r2﹣r﹣4=0
解得r1=
 ,r2=
,r2= (舍去),
(舍去),∴此圆的半径为
 ;
;②当圆位于x轴下方时,
同理可求得圆的半径为
 .
.综上所述,此圆的半径为
 或
或



练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•自贡)如图,抛物线l交x轴于点A(-3,0)、B(1,0),交y轴于点C(0,-3).将抛物线l沿y轴翻折得抛物线l1.
(2012•自贡)如图,抛物线l交x轴于点A(-3,0)、B(1,0),交y轴于点C(0,-3).将抛物线l沿y轴翻折得抛物线l1.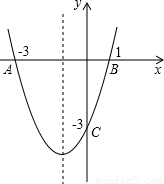
 :
: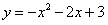 交x轴于A、B两点,交y轴于M点,抛物线
交x轴于A、B两点,交y轴于M点,抛物线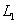 向右平移2个单位后得到抛物线
向右平移2个单位后得到抛物线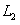 ,
,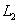 交x轴于C、D两点。
交x轴于C、D两点。 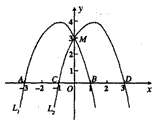
 对应的函数表达式;
对应的函数表达式;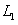 或
或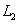 在x轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由;
在x轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由;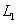 上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线
上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线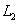 上,请说明理由。
上,请说明理由。