Question

【题目】某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，有如下探讨：

甲同学：我发现这种多边形不一定是正多边形．如圆内接矩形不一定是正方形．

乙同学：我知道边数为3时，它是正三角形；我想，边数为5时，它可能也是正五边形…

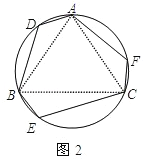
丙同学：我发现边数为6时，它也不一定是正六边形．如图2，△ABC是正三角形，弧AD、弧BE、弧CF均相等，这样构造的六边形ADBECF不是正六边形．

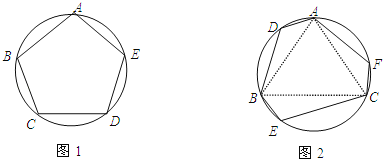
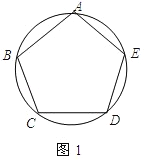
（1）如图1，若圆内接五边形ABCDE的各内角均相等，则∠ABC= °，并简要说明圆内接五边形ABCDE为正五边形的理由；

（2）如图2，请证明丙同学构造的六边形各内角相等；

（3）根据以上探索过程，就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n（n≥3，n为整数）”的关系，提出你的猜想（不需证明）．

Answer 1

【答案】（1）108．见解析；（2）见解析；（3）见解析

【解析】

试题分析：（1）运用n边形的内角和定理就可求出∠ABC的度数；已知圆内接五边形ABCDE的各内角均相等，要证该五边形为正五边形，只需证该五边形的各边均相等，只需利用弧与圆周角之间的等量关系就可解决问题．

（2）由△ABC是正三角形可得∠ABC=∠ACB=∠BAC=60°，根据圆内接四边形的性质可得∠AFC、∠ADB、∠BEC均为120°，由=可得∠ABD=∠CAF，即可求出∠DAF=120°，同理可得∠DBE=∠ECF=120°，问题得以解决．

（3）依据对（1）、（2）的探索积累的经验就可提出合理的猜想．

解：（1）∵五边形的内角和=（5﹣2）×180°=540°，

∴∠ABC==108°．

故答案为：108．

理由：如图1，

∵∠A=∠B

∴=，

∴﹣=﹣，

∴=，

∴BC=AE．

同理可得：BC=DE，DE=AB，AB=CD，CD=AE，

∴BC=DE=AB=CD=AE，

∴五边形ABCDE是正五边形；

（2）证明：如图2，

∵△ABC是正三角形，

∴∠ABC=∠ACB=∠BAC=60°，

∵四边形ABCF是圆内接四边形，

∴∠ABC+∠AFC=180°，

∴∠AFC=120°．

同理可得：∠ADB=120°，∠BEC=120°．

∵∠ADB=120°，

∴∠DAB+∠ABD=60°．

∵=，

∴∠ABD=∠CAF，

∴∠DAB+∠CAF=60°，

∴∠DAF=∠DAB+∠CAF+∠BAC=120°．

同理可得：∠DBE=120°，∠ECF=120°，

∴∠AFC=∠ADB=∠BEC=∠DAF=∠DBE=∠ECF=120°，

故图2中六边形各角相等；

（3）由（1）、（2）可提出以下猜想：

当n（n≥3，n为整数）是奇数时，各内角都相等的圆内接多边形是正多边形；

当n（n≥3，n为整数）时偶数时，各内角都相等的圆内接多边形不一定为正多边形．