题目内容
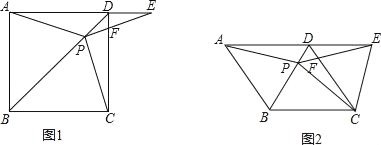
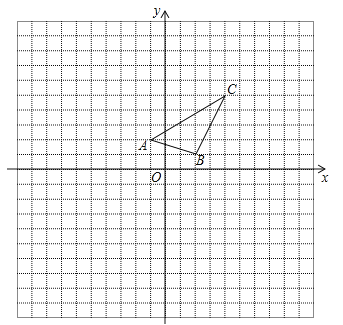
【题目】如图1,在平面直角坐标系中,已知点![]() ,点
,点![]() ,
,![]() 为线段
为线段![]() 上一点,且满足
上一点,且满足![]() .
.
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
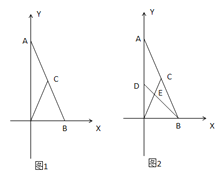
(2)如图2,![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,试探索
,试探索![]() 是否为定值?若是,求出该值;若不是,请说明理由;
是否为定值?若是,求出该值;若不是,请说明理由;
(3)点![]() 为坐标轴上一点,请直接写出满足
为坐标轴上一点,请直接写出满足![]() 为等腰三角形的所有点
为等腰三角形的所有点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)是定值,定值为2;(3)
;(2)是定值,定值为2;(3)![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)利用“待定系数法”可求出解析式,然后过点C作CF⊥OB,利用等腰三角形的性质求出点C横坐标,再利用解析式求出点C坐标即可;
(2)先利用勾股定理计算出AB、OC长,从而证明OC=BC=AC,再利用“等边对等角”得到∠CAO=∠AOC,最后利用三角形外角定理即可得到结果;
(3)分BP=BC、CP=CB、PB=PC三种情况讨论,分别进行计算即可.
解:(1)设![]() :
:![]() ,
,
代入点![]() 、
、![]() 可得
可得![]() ,
,
解得:![]() ,
,
即![]() :
:![]() ,
,
设![]() ,如图作
,如图作![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
将点![]() 代入
代入![]() 可得:
可得:![]() ,
,
∴![]() ;
;
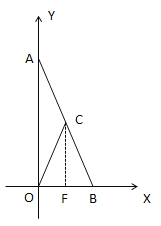
(2)是定值,定值为2.
由(1)可得![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
又∵在![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(3)①BC=BP=![]() 时:
时:
当点P在x轴上时,OP=![]() 或
或![]() ,此时
,此时![]() ,
,![]() ,
,
当点P在y轴上时,在Rt△OBP中,OP=![]() ,此时
,此时![]() ,
,![]() ,
,
②CB=CP=![]() 时:
时:
由(2)知OC=![]() ,
,
∴CP=OC,此时![]() ,
,
③PB=PC时:
当P在x轴上时,设P(x,0),则![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
此时![]() ,
,
当P在y轴上时,设P(0,y),则![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
此时![]() ,
,
综上,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

 举一反三单元同步过关卷系列答案
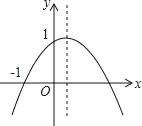
举一反三单元同步过关卷系列答案【题目】小明同学在用描点法画二次函数y=x2+bx+c图像时,由于粗心他算错了一个y值,列出了下面表格:
x | … | -1 | 0 | 1 | 2 | 3 | … |
y=x2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
(1)请你帮他指出这个错误的y值,并说明理由;
(2)若点M(m,y1),N(m+4,y2)在二次函数y=x2+bx+c图像上,且m>-1,试比较y1与y2的大小.