题目内容
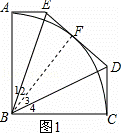
五边形ABCDE中,∠EAB=∠ABC=∠BCD=90°,AB=BC,且满足以点B为圆心,AB长为半径的圆弧AC与边DE相切于点F,连接BE,BD.
(1)如图1,求∠EBD的度数;
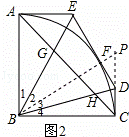
(2)如图2,连接AC,分别与BE,BD相交于点G,H,若AB=1,∠DBC=15°,求AG•HC的值.
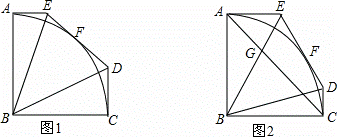
解:(1)如图1,连接BF,
∵DE与⊙B相切于点F,
∴BF⊥DE,
在Rt△BAE与Rt△BEF中,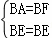 ,
,
∴Rt△BAE≌Rt△BEF,
∴∠1=∠2,
同理∠3=∠4,
∵∠ABC=90°,
∴∠2+∠3=45°,
即∠EBD=45°;
(2)如图2,连接BF并延长交CD的延长线于P,
∵∠4=15°,
由(1)知,∠3=∠4=15°,
∴∠1=∠2=30°,∠PBC=30°,
∵∠EAB=∠PCB=90°,AB=1,
∴AE=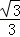 ,BE=
,BE=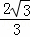 ,
,
在△ABE与△PBC中,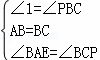 ,
,
∴△ABE≌△PBC,
∴PB=BE=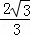 ,
,
∴PF=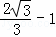 ,
,
∵∠P=60°,
∴DF=2﹣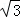 ,
,
∴CD=DF=2﹣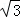 ,
,
∵∠EAG=∠DCH=45°,
∠AGE=∠BDC=75°,
∴△AEG∽△CHD,
∴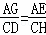 ,
,
∴AG•CH=CD•AE,
∴AG•CH=CD•AE=(2﹣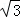 )•
)•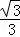 =
=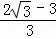 .
.

练习册系列答案
相关题目
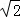 ≈1.4,
≈1.4,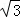 ≈1.7)
≈1.7)
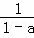 称为a的差倒数,如:2的差倒数为
称为a的差倒数,如:2的差倒数为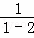 =﹣1;﹣1的差倒数是
=﹣1;﹣1的差倒数是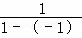 =
=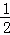 ;已知a1=3,a2是a1的差倒数,a3是a2的差倒数.a4是a3差倒数,…依此类推,则a2015=
;已知a1=3,a2是a1的差倒数,a3是a2的差倒数.a4是a3差倒数,…依此类推,则a2015=