题目内容
已知:AB是⊙O的弦,D是AB的中点,过B作AB的垂线交AD的延长线于C.
(1)求证:AD=DC;
(2)过D作 ⊙O 的切线交BC于E,若DE=EC,求sinC.
 |
证明:连BD∵ ∴∠A=∠ABD∴AD=BD
∴∠A=∠ABD∴AD=BD
∵∠A+∠C=90°,∠DBA+∠DBC=90°∴∠C=∠DBC∴BD=DC
∴AD=DC
(2)连接OD∵DE为⊙O切线 ∴OD⊥DE
∵ ,OD过圆心 ∴OD⊥AB
,OD过圆心 ∴OD⊥AB
又∵AB⊥BC ∴四边形FBED为矩形∴DE⊥BC
∵BD为Rt△ABC斜边上的中线∴BD=DC ∴BE=EC=DE
∴∠C=45°
∴sin∠C=

练习册系列答案
相关题目
 ,1)关于x轴对称的点的坐标是
,1)关于x轴对称的点的坐标是 ) D (1.
) D (1.
 .将142000平方米用科学用科学记数法表示是 平方米
.将142000平方米用科学用科学记数法表示是 平方米
 A.80° B.85° C.95° D.110°
A.80° B.85° C.95° D.110° .
.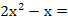 ______________
______________