题目内容
 (2013•济南)如图,点A的坐标是(-2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.
(2013•济南)如图,点A的坐标是(-2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.(1)求直线BD的函数表达式;
(2)求线段OF的长;
(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.
分析:(1)根据△OBC是等边三角形,可得∠OBC=60°,在Rt△PBD中,解得OD的长度,得出点D的坐标,利用待定系数法求出直线BD的解析式即可;
(2)分别求出∠BAE和∠AFO的度数,即可得出OF=OA=2.
(3)在Rt△ABE中,先求出BE,继而得出CE=OF,证明△COE≌△OBF,可得BF和OE的数量关系.
(2)分别求出∠BAE和∠AFO的度数,即可得出OF=OA=2.
(3)在Rt△ABE中,先求出BE,继而得出CE=OF,证明△COE≌△OBF,可得BF和OE的数量关系.
解答:解:(1)∵△OBC是等边三角形,
∴∠OBC=60°,OC=BC=0B,
∵点B的坐标为(6,0),
∴OB=6,
在Rt△OBD中,∠OBC=60°,OB=6,
∴∠ODB=30°,
∴BD=12,
∴OD=
=6
,
∴点D的坐标为(0,6
),
设直线BD的解析式为y=kx+b,则可得
,
解得:
,
∴直线BD的函数解析式为y=-
x+6
.
(2)∵∠OCB=60°,∠CEF=90°,
∴∠CFE=30°,
∴∠AFO=30°(对顶角相等),
又∵∠OBC=60°,∠AEB=90°,
∴∠BAE=30°,
∴∠BAE=∠AFO,
∴OF=OA=2.
 (3)连接BF,OE,如图所示:
(3)连接BF,OE,如图所示:
∵A(-2,0),B(6,0),
∴AB=8,
在Rt△ABE中,∠ABE=60°,AB=8,
∴BE=ABcos∠ABE=4,
∴CE=BC-BE=2,
∴OF=CE=2,
在△COE和△OBF中,
,
∴△COE≌△OBF(SAS),
∴OE=BF.
∴∠OBC=60°,OC=BC=0B,
∵点B的坐标为(6,0),
∴OB=6,
在Rt△OBD中,∠OBC=60°,OB=6,
∴∠ODB=30°,
∴BD=12,
∴OD=
| 122-62 |
| 3 |
∴点D的坐标为(0,6
| 3 |
设直线BD的解析式为y=kx+b,则可得
|
解得:
|
∴直线BD的函数解析式为y=-
| 3 |
| 3 |
(2)∵∠OCB=60°,∠CEF=90°,
∴∠CFE=30°,
∴∠AFO=30°(对顶角相等),
又∵∠OBC=60°,∠AEB=90°,
∴∠BAE=30°,
∴∠BAE=∠AFO,
∴OF=OA=2.
 (3)连接BF,OE,如图所示:
(3)连接BF,OE,如图所示:∵A(-2,0),B(6,0),
∴AB=8,
在Rt△ABE中,∠ABE=60°,AB=8,
∴BE=ABcos∠ABE=4,
∴CE=BC-BE=2,
∴OF=CE=2,
在△COE和△OBF中,
|
∴△COE≌△OBF(SAS),
∴OE=BF.
点评:本题考查了一次函数的综合,解答本题的关键是熟练掌握待定系数法及数形结合思想的运用,对于此类综合性较强的题目,要求同学们具有扎实的基本功,熟练掌握学过的性质定理及常见解题方法.

练习册系列答案
相关题目
 (2013•济南)如图,直线a,b被直线c所截,a∥b,∠1=130°,则∠2的度数是( )
(2013•济南)如图,直线a,b被直线c所截,a∥b,∠1=130°,则∠2的度数是( )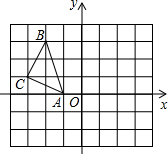 (2013•济南)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,3),C(-3,1),将△ABC绕点A按顺时针方向旋转90°,得到△AB′C′,则点B′的坐标为( )
(2013•济南)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,3),C(-3,1),将△ABC绕点A按顺时针方向旋转90°,得到△AB′C′,则点B′的坐标为( )