题目内容
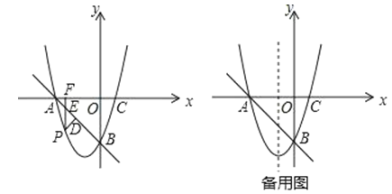
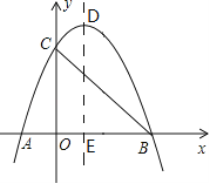
【题目】如图,抛物线![]() 与x轴交于点A(-1,0),B(3,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴与点E,则下列结论:①2a+b=0;②b+2c>0;③a+b>am
与x轴交于点A(-1,0),B(3,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴与点E,则下列结论:①2a+b=0;②b+2c>0;③a+b>am![]() +bm(m为任意实数);④一元二次方程
+bm(m为任意实数);④一元二次方程![]() 有两个不相等的实数根;⑤当△BCD为直角三角形时,a的值有2个;⑥若点P为对称轴上的动点,则
有两个不相等的实数根;⑤当△BCD为直角三角形时,a的值有2个;⑥若点P为对称轴上的动点,则![]() 有最大值,最大值为
有最大值,最大值为![]() .其中正确的有( )
.其中正确的有( )
A.2个B.3个C.4个D.5个
【答案】C
【解析】
由A(-1,0),B(3,0)得出抛物线的对称轴,利用对称轴判断①,利用对称轴与函数的最大值判断②,利用不同的![]() 的值对应不同的函数值,数型结合判断③,利用两个函数的交点判断④,利用两条直线互相垂直时,
的值对应不同的函数值,数型结合判断③,利用两个函数的交点判断④,利用两条直线互相垂直时,![]() 求出
求出![]() 的值判断⑤,利用三角形任意两边的差小于第三边,判断⑥.
的值判断⑤,利用三角形任意两边的差小于第三边,判断⑥.
解:因为A(-1,0),B(3,0),所以抛物线的对称轴是![]() ,所以
,所以![]() ,
,
从而①2a+b=0正确.
又因为当![]() ,
,![]() >0,把2a+b=0化为
>0,把2a+b=0化为![]() 代入
代入![]() >0得:
>0得:![]() >0,即b+2c>0,所以②正确.
>0,即b+2c>0,所以②正确.
又因为当![]() ,
,![]() ,当
,当![]() ,
,![]() ,由抛物线的性质知道:函数的最大值是
,由抛物线的性质知道:函数的最大值是![]() ,所以
,所以![]() 为任意实数时有
为任意实数时有![]() ,所以
,所以![]() ,所以③错误.
,所以③错误.
由![]() 化为
化为![]() ,考查函数
,考查函数![]() 与
与![]() 的交点个数,显然两个函数有两个交点,所以④一元二次方程
的交点个数,显然两个函数有两个交点,所以④一元二次方程![]() 有两个不相等的实数根正确.
有两个不相等的实数根正确.
因为抛物线过点A(-1,0),B(3,0),
所以:![]() 解得:
解得:![]()
所以抛物线为![]()
所以C(0,![]() ),D(1,
),D(1,![]() )而B(3,0)
)而B(3,0)
所以![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,解得:
,解得:![]() ,(
,(![]() 舍去)
舍去)
当![]() 时,
时,![]() ,解得:
,解得:![]() ,(
,(![]() 舍去)
舍去)
当![]() 时,
时,![]() ,方程无解,所以⑤正确.
,方程无解,所以⑤正确.
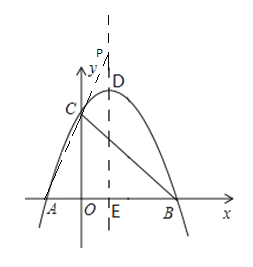
如下图,因为A,B两点关于抛物线的对称轴![]() 对称,所以
对称,所以![]() =
=![]() ,当P,A,C三点不共线时总有
,当P,A,C三点不共线时总有![]() <AC,而且只有P,A,C三点共线时有
<AC,而且只有P,A,C三点共线时有![]() =AC,所以
=AC,所以![]() 有最大值且等于AC,又因为A(-1,0),C(0,c),所以
有最大值且等于AC,又因为A(-1,0),C(0,c),所以![]() ,故⑥错误.
,故⑥错误.
故选C.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目