题目内容
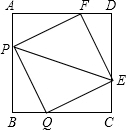
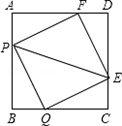
如图所示,有四个动点P,Q,E,F分别从面积为4的正方形ABCD的顶点A,B,C,D同时出发,沿着AB,BC,CD,DA以同样的速度向B,C,D,A移动.
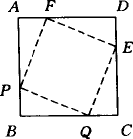
(1)证明四边形PQEF是正方形;
(2)PE是否总过某一定点?说明理由;
(3)四边形PQEF的顶点位于何处,其面积是否有最小值?最小值是多少?
答案:
解析:
解析:
|
(1)证△PAF≌△QBP≌△ECQ≌△FDE即可. (2)PE总经过AC的中点,连结AC,PE,设PE与AC相交于点O,则△APO≌△CEO.故AO=CO. 故O是正方形ABCO的中心,∴PE过一定点. (3)当四边形PQEF的顶点位于各边中点时,其面积最小,最小面积为2. 设AF=PB=CQ=DE=x,则AP=BQ=CE=DF=2-x. 则四边形PQEF的面积S可用x2+(2-x)2表示. 即S=2x2-4x+4=2(x-1)2+2,故当x=1时,面积有最小值为2. |

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
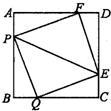 40、如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.
40、如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.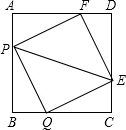 如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.
如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.