题目内容
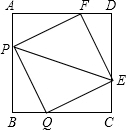
如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.
(1)试判断四边形PQEF是否是正方形,并证明;
(2)PE是否总过某一定点,并说明理由.
(1)试判断四边形PQEF是否是正方形,并证明;
(2)PE是否总过某一定点,并说明理由.
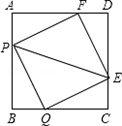
| 解:(1)在正方形ABCD中,AP=BQ=CE=DF,AB=BC=CD=DA, ∴BP=QC=ED=FA. 又∵∠BAD=∠B=∠BCD=∠D=90°, ∴△AFP≌△BPQ≌△CQE≌△DEF. ∴FP=PQ=QE=EF,∠APF=∠PQB. ∴四边形PQEF是菱形, ∵∠FPQ=90°, ∴四边形PQEF为正方形. (2)连接AC交PE于O, ∵AP平行且等于EC, ∴四边形APCE为平行四边形. ∵O为对角线AC的中点, ∴对角线PE总过AC的中点. |
 |

练习册系列答案
相关题目
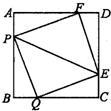 40、如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.
40、如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.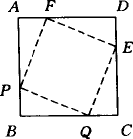
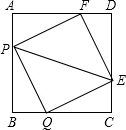 如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.
如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.