题目内容
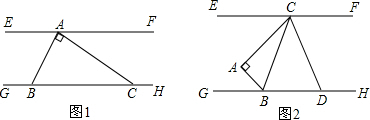
17.直线EF、GH之间有一个直角三角形ABC,其中∠BAC=90°,∠ABC=α.(1)如图1,点A在直线EF上,B、C在直线GH上,若∠α=60°,∠FAC=30°.求证:EF∥GH;
(2)将三角形ABC如图2放置,直线EF∥GH,点C、B分别在直线EF、GH上,且BC平分∠ABH,直线CD平分∠FCA交直线GH于D.在α取不同数值时,∠BCD的大小是否发生变化?若不变求其值,若变化指出其变化范围.
分析 (1)求出∠EAB,推出∠EAB=∠ABC,根据平行线的判定推出即可;
(2)求出AM∥EF∥GH,根据平行线的性质得出∠FCA+∠CAM=180°,∠MAB+∠ABH=180°,∠CBH=∠ECB,求出∠FCA+∠ABH=270°,求出∠FCD+∠ECB=135°,根据三角形内角和定理求出即可.
解答 (1)证明:∵∠EAB=180°-∠BAC-∠FAC,∠BAC=90°,∠FAC=30°,
∴∠EAB=60°,
又∵∠ABC=60°,
∴∠EAB=∠ABC,
∴EF∥GH;
(2)解:不发生变化,
理由是:经过点A作AM∥GH,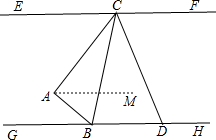
又∵EF∥GH,
∴AM∥EF∥GH,
∴∠FCA+∠CAM=180°,∠MAB+∠ABH=180°,∠CBH=∠ECB,
又∵∠CAM+∠MAB=∠BAC=90°,
∴∠FCA+∠ABH=270°,
又∵BC平分∠ABH,CD平分∠FCA,
∴∠FCD+∠CBH=135°,
又∵∠CBH=∠ECB,即∠FCD+∠ECB=135°,
∴∠BCD=180°-(∠FCD+∠ECB)=45°.
点评 本题考查了三角形内角和定理,平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,难度适中.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
5.下列数值中是不等式2x+3>9的解的是( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
12.武汉东湖高新开发区某企业新增了一个项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.设购买A种型号的污水处理设备x台,可列不等式组$\left\{\begin{array}{l}{12x+10(8-x)≤89}\\{200x+160(8-x)≥1380}\end{array}\right.$.
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 月污水处理能力(吨/月) | 200 | 160 |
6.今年我市有近2万名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这1000名考生是总体的一个样本 | B. | 近2万名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 1000名学生是样本容量 |
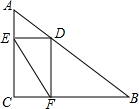 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )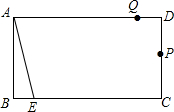 如图,矩形ABCD中,AB=6cm,BC=10cm,动点P从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点Q从点D出发,按折线DABCD方向以1cm/s的速度运动.若点E在线段BC上,且BE=1cm,若动点P、Q同时出发,经过几秒钟,点A、E、P、Q组成平行四边形?
如图,矩形ABCD中,AB=6cm,BC=10cm,动点P从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点Q从点D出发,按折线DABCD方向以1cm/s的速度运动.若点E在线段BC上,且BE=1cm,若动点P、Q同时出发,经过几秒钟,点A、E、P、Q组成平行四边形?