题目内容
 (2012•普陀区一模)如图,梯形OABC,BC∥OA,边OA在x轴正半轴上,边OC在y轴正半轴上,点B(3,4),AB=5.
(2012•普陀区一模)如图,梯形OABC,BC∥OA,边OA在x轴正半轴上,边OC在y轴正半轴上,点B(3,4),AB=5.(1)求∠BAO的正切值;
(2)如果二次函数y=
| 4 | 9 |
(3)点Q在x轴上,以点Q,点O及(2)中的点M为顶点的三角形与△ABO相似,求点Q的坐标.
分析:(1)作BD⊥OA于点D,由点B的坐标可以求出BD、OD的值,在直角三角形ABD中由勾股定理可以求出AD的值,从而可以求出∠BAO的正切值.
(2)由条件可以求出A点的坐标,利用待定系数法就可以直接求出抛物线的解析式.
(3)根据条件当△ABO∽△MQO和△ABO∽△QMO时,从两种情况根据相似三角形的性质就可以求出OQ的值,从而求出Q点的坐标.
(2)由条件可以求出A点的坐标,利用待定系数法就可以直接求出抛物线的解析式.
(3)根据条件当△ABO∽△MQO和△ABO∽△QMO时,从两种情况根据相似三角形的性质就可以求出OQ的值,从而求出Q点的坐标.
解答:解:(1)作BD⊥OA于点D,
∴∠ADB=90°,
∴在Rt△ABD中,由勾股定理得
AD2=AB2-BD2
∵B(3,4),
∴OD=3,BD=4.
∵AB=5,
∴AD2=25-16,
∴AD=3,
∴tan∠BAD=
.

(2)∵AD=3,OD=3,
∴OA=6,
∴A(6,0),O(0,0)
∴
∴
∴抛物线的解析式为:y=
x2-
x
∴y=
(x -3)2-4,
∴M(3,-4).
(3)∵M(3,-4),B(3,4),
∴OB=OM,
∵BD⊥OA,OD=AD,
∴OB=AB=5,
∴OM=5.
△ABO∽△MQO时,
=
,
∴
=
,
∴OQ=
,
∴Q(
,0)
△ABO∽△QMO时,
=
,
∴
=
,
∴QO=6,
∴Q(6,0),
综上所述,所以Q(
,0)或(6,0)

∴∠ADB=90°,
∴在Rt△ABD中,由勾股定理得
AD2=AB2-BD2
∵B(3,4),
∴OD=3,BD=4.
∵AB=5,
∴AD2=25-16,
∴AD=3,
∴tan∠BAD=
| 4 |
| 3 |

(2)∵AD=3,OD=3,
∴OA=6,
∴A(6,0),O(0,0)
∴
|
∴
|
∴抛物线的解析式为:y=
| 4 |
| 9 |
| 8 |
| 3 |
∴y=
| 4 |
| 9 |
∴M(3,-4).
(3)∵M(3,-4),B(3,4),
∴OB=OM,
∵BD⊥OA,OD=AD,
∴OB=AB=5,
∴OM=5.
△ABO∽△MQO时,
| AO |
| MO |
| BO |
| OQ |
∴
| 6 |
| 5 |
| 5 |
| OQ |
∴OQ=
| 25 |
| 6 |
∴Q(
| 25 |
| 6 |
△ABO∽△QMO时,
| AO |
| QO |
| BO |
| MO |
∴
| 6 |
| QO |
| 5 |
| 5 |
∴QO=6,
∴Q(6,0),
综上所述,所以Q(
| 25 |
| 6 |

点评:本题考查了坐标与图形的性质,锐角三角函数的运用,勾股定理的运用,待定系数法求二次函数的解析式,相似三角形的判定与性质.

练习册系列答案
相关题目
 (2012•普陀区一模)如图,由5个同样大小的正方形合成一个矩形,那么∠ABD+∠ADB的度数是( )
(2012•普陀区一模)如图,由5个同样大小的正方形合成一个矩形,那么∠ABD+∠ADB的度数是( ) (2012•普陀区一模)如图是一张直角三角形的纸片,直角边AC=6cm,
(2012•普陀区一模)如图是一张直角三角形的纸片,直角边AC=6cm,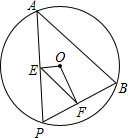 (2012•普陀区一模)如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.
(2012•普陀区一模)如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.