Question

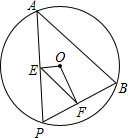（2012•普陀区一模）如图，点A，B是⊙O上两点，AB=10，点P是⊙O上的动点（P与A，B不重合），连接AP，BP，过点O分别作OE⊥AP，OF⊥BP，点E、F分别是垂足．
（1）求线段EF的长；
（2）点O到AB的距离为2，求⊙O的半径．

Answer 1

分析：（1）由于OE⊥AP，OF⊥BP，点E、F分别是垂足，根据垂径定理可以得到E、F分别是AP、BP的中点，然后利用中位线定理即可求解；
（2）如图，过O作OC⊥AB于C，连接OB，利用垂径定理和勾股定理即可求解．

解答：解：（1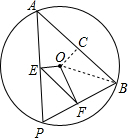）∵OE⊥AP，OF⊥BP，点E、F分别是垂足，
∴AE=EP，PF=BF，
∴EF=

1

2

AB，而AB=10，
∴EF=5；

（2）如图，过O作OC⊥AB于C，连接OB，
∴C为AB的中点，
∴BC=5，
而OC=2，
∴OB=

22+52

=

29

，
∴⊙O的半径为

29

．

点评：此题考查了垂径定理和勾股定理，解题时首先根据垂径定理证明中位线，然后利用勾股定理计算即可解决问题．